In questo articolo descriviamo come implementare il clustering dei titoli azionari con l’algoritmo K-means in Python. In particolare implementiamo uno script per scaricare i dati sui prezzi per le azioni S&P 500, calcolare i rendimenti e volatilità storici, quindi applicare l’algoritmo di clustering K-Means, già descritto nel tutorial, in modo da suddividere le azioni in gruppi distinti basati sui rendimenti e sulle volatilità.
L’algoritmo K-means
Dividere le azioni in gruppi con “caratteristiche simili” può aiutarci nella costruzione di portafogli e nell’asset management. E’ uno buon metodo per scegliere un universo di azioni con una sufficiente diversificazione tra di loro.
L’obiettivo dell’algoritmo è minimizzare la varianza totale intra-gruppo; ogni gruppo viene identificato mediante un centroide o punto medio. L’algoritmo segue una procedura iterativa: inizialmente crea k partizioni e assegna i punti d’ingresso a ogni partizione o casualmente o usando alcune informazioni euristiche; quindi calcola il centroide di ogni gruppo; costruisce in seguito una nuova partizione associando ogni punto d’ingresso al gruppo il cui centroide è più vicino ad esso; infine vengono ricalcolati i centroidi per i nuovi gruppi e così via, finché l’algoritmo non converge.
Vediamo il codice Python necessario per eseguire scaricare e raccogliere i dati e quindi procedere con la manipolazione e l’analisi dei dati.
Il codice
Per prima cosa, dobbiamo acquisire i dati da analizzare. Prevediamo l’importazioni dei moduli ed implementiamo le funzioni per il download dei dati storici per i ticker dei titoli che compongono l’S&P 500.
import numpy as np
import pandas as pd
import yfinance as yf
from math import sqrt
from sklearn.cluster import KMeans
from scipy.cluster.vq import kmeans,vq
from matplotlib import pyplot as plt
import seaborn as sns
sns.set_style('whitegrid')
sp500_url = 'https://en.wikipedia.org/wiki/List_of_S%26P_500_companies'
# Legge url ed estrae i dati dei ticker
data_table = pd.read_html(sp500_url)
tickers = data_table[0][1:]['Symbol'].to_list()
prices_list = []
# Scarica i dati storici dei ticker
for ticker in tickers:
try:
prices = yf.download(ticker, '2017-01-01')['Adj Close']
prices = pd.DataFrame(prices)
prices.columns = [ticker]
prices_list.append(prices)
except:
pass
prices_df = pd.concat(prices_list,axis=1)
prices_df.sort_index(inplace=True)
print(prices_df.head())
Otteniamo qualcosa di simile a quanto segue:
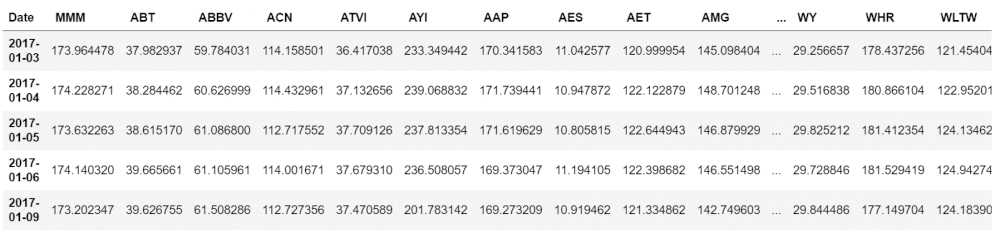
Possiamo iniziare ad analizzare i dati e quindi ad applicare l’algoritmo K-Means…
Dobbiamo prima di tutto scegliere in quanti cluster vogliamo suddividere i dati. Invece di prendere una decisione arbitraria, possiamo usare una “curva a gomito” (Elbow Curve) per evidenziare la relazione tra il numero di cluster usati e la somma degli errori al quadrato (SSE) ottenuti usando quel numero di cluster. Visualizziamo questa curva per poter identificare il numero di cluster ottimale da usare – dobbiamo cercare un compromesso tra il minor numero di cluster e il minor valore dell’SSE.
Il seguente codice implementa il calcolo e la visualizzazione della Elbow Curve.
# Calcola la media e la volatilità annuale dei rendimenti percentuali
returns = prices_df.pct_change().mean() * 252
returns = pd.DataFrame(returns)
returns.columns = ['Returns']
returns['Volatility'] = prices_df.pct_change().std() * sqrt(252)
# Formattazione dei dati come un array numpy per l'algoritmo K-Means
data = np.asarray([np.asarray(returns['Returns']),np.asarray(returns['Volatility'])]).T
X = data
distorsions = []
for k in range(2, 20):
k_means = KMeans(n_clusters=k)
k_means.fit(X)
distorsions.append(k_means.inertia_)
fig = plt.figure(figsize=(15, 5))
plt.plot(range(2, 20), distorsions)
plt.grid(True)
plt.title('Elbow curve')
plt.show()
Otteniamo il seguente grafico:
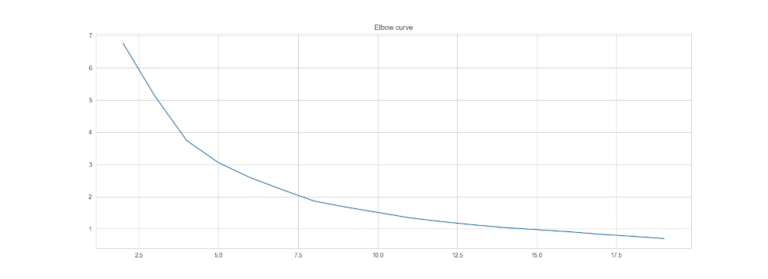
Dal grafico possiamo vedere che quando il numero di cluster raggiunge 5 (sull’asse inferiore), la riduzione dell’SSE inizia a diminuire all’aumentare del numero di cluster. Possiamo quindi ipotizzare che il numero di cluster ottimale per questo insieme di dati è intorno a 5.
I risultati
Usiamo questo valore per l’algoritmo K-means
# Calcolo del K-Means con K = 5 (5 clusters)
centroids,_ = kmeans(data,5)
# Assegnazione di ogni titolo a un cluster
idx,_ = vq(data,centroids)
# Grafici usando la logica di indicazzazione di numpy
plt.plot(data[idx==0,0],data[idx==0,1],'ob',
data[idx==1,0],data[idx==1,1],'oy',
data[idx==2,0],data[idx==2,1],'or',
data[idx==3,0],data[idx==3,1],'og',
data[idx==4,0],data[idx==4,1],'om')
plt.plot(centroids[:,0],centroids[:,1],'sg',markersize=8)
plt.show()
Vediamo quindi la seguente classificazione
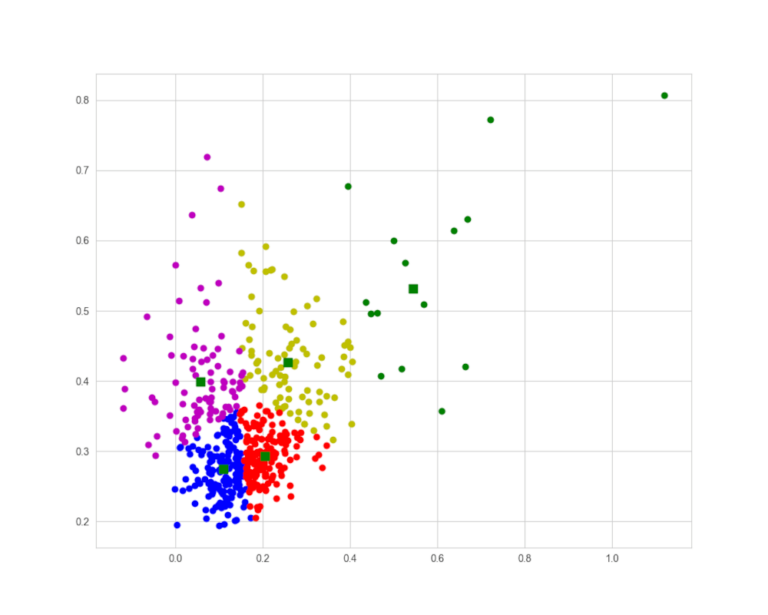
Infine, per sapere il cluster di appartenenza di ogni titolo possiamo eseguire la seguente riga di codice per analizzare i risultati del k-means e costruire una lista di tuple nel formato (Nome del Titolo, Numero del Cluster):
details = [(name, cluster) for name, cluster in zip(returns.index, idx)]
for detail in details:
print(detail)
Il codice stampa qualcosa di simile al seguente (non ho incluso tutti i risultati per brevità)
('AOS', 3)
('ABT', 1)
('ABBV', 1)
('ACN', 1)
('ATVI', 1)
('ADM', 1)
('ADBE', 4)
('ADP', 1)
('AAP', 3)
('AES', 1)
('AFL', 1)
('A', 1)
('APD', 1)
('AKAM', 3)
('ALK', 2)
('ALB', 4)
('ARE', 3)
('ALGN', 4)
('ALLE', 1)
('LNT', 3)
('ALL', 3)
('GOOGL', 1)
('GOOG', 1)
('MO', 3)
('AMZN', 4)
('AMCR', 3)
...
Abbiamo ottenuto una lista dei titoli dell’S&P 500, insieme a uno dei 5 cluster a cui appartengono. I cluster sono definiti i base alle caratteristiche di rendimento e volatilità dei titoli. Abbiamo anche previsto una rappresentazione visiva dei cluster tramite un grafico.
Codice completo
In questo articolo abbiamo descritto come implementare il clustering dei titoli azionari con l’algoritmo K-means in Python. Per il codice completo riportato in questo articolo, si può consultare il seguente repository di github:
https://github.com/datatrading-info/MachineLearning