Nell’articolo precedente abbiamo descritto una funzione Python che usa l’API di Polygon per estrarre un mese di dati intraday per una coppia FX, sia principale (EURUSD) che esotica (MZXZAR). Abbiamo tracciato le serie dei rendimenti e esaminato alcuni dei problemi che possono verificarsi quando si lavora con questo tipo di dati. Questo articolo fa parte di un tutorial dove vediamo come creare un modello di apprendimento automatico basato sulla volatilità realizzata per prevedere il cambiamento del regime del mercato.
In questo articolo descriviamo come calcolare la volatilità realizzata con i dati Forex di Polygon. Effettuiamo anche un’analisi esplorativa dei dati in modo da preparare il set di funzionalità per il modello di apprendimento automatico.
Per eseguire il codice descritto in questo articolo abbiamo bisogno di:
- Python 3.9
- Matplotlib 3.5
- Pandas 1.4
- Requests 2.27
- Seaborn 0.12.
Consigliamo inoltre di dare un’occhiata agli altri tutorial sul Trading Algoritmico disponibili su DataTrading.info.
Volatilità realizzata
Per calcolare la volatilità realizzata dobbiamo prima ottenere e formattare i dati. Nell’articolo precedente abbiamo creato le funzioni Python per contattare l’API Polygon e ottenere un mese di dati intraday per EURUSD e MZXZAR. Di seguito riportiamo il codice per ottenere i dati.
import os
import json
import matplotlib.pyplot as plt
import pandas as pd
import requests
import seaborn as sns
POLYGON_API_KEY = os.getenv("POLYGON_API_KEY")
HEADERS = {
'Authorization': 'Bearer ' + POLYGON_API_KEY
}
BASE_URL = 'https://api.polygon.io/v2/aggs/'
def get_fx_pairs_data(pg_tickers):
start = '2023-01-01'
end = '2023-01-31'
multiplier = '1'
timespan = 'minute'
fx_url = f"range/{multiplier}/{timespan}/{start}/{end}?adjusted=true&sort=asc&limit=50000"
fx_pairs_dict = {}
for pair in pg_tickers:
response = requests.get(
f"{BASE_URL}ticker/{pair}/{fx_url}",
headers=HEADERS
).json()
fx_pairs_dict[pair] = pd.DataFrame(response['results'])
return fx_pairs_dict
def format_fx_pairs(fx_pairs_dict):
for pair in fx_pairs_dict.keys():
fx_pairs_dict[pair]['t'] = pd.to_datetime(fx_pairs_dict[pair]['t'],unit='ms')
fx_pairs_dict[pair] = fx_pairs_dict[pair].set_index('t')
return fx_pairs_dict
def create_str_index(fx_pairs_dict):
fx_pairs_str_ind = {}
for pair in fx_pairs_dict.keys():
fx_pairs_str_ind[pair] = fx_pairs_dict[pair].set_index(
fx_pairs_dict[pair].index.to_series().dt.strftime(
'%Y-%m-%d-%H-%M-%S'
)
)
return fx_pairs_str_ind
def create_returns_series(fx_pairs_str_ind):
for pair in fx_pairs_str_ind.keys():
fx_pairs_str_ind[pair]['rets'] = fx_pairs_str_ind[pair]['c'].pct_change()
return fx_pairs_str_ind
Le funzioni possono essere chiamate in una main. Il codice seguente memorizza il valore restituito da ciascuna funzione in una variabile.
pg_tickers = ["C:EURUSD", "C:MXNZAR"]
fx_pairs_dict = get_fx_pairs_data(pg_tickers)
formatted_fx_dict = format_fx_pairs(fx_pairs_dict)
fx_pairs_str_ind = create_str_index(formatted_fx_dict)
fx_returns_dict = create_returns_series(fx_pairs_str_ind)
È possibile accedere ai dati FX per ciascuna coppia come segue:
print(fx_returns_dict['C:EURUSD'])
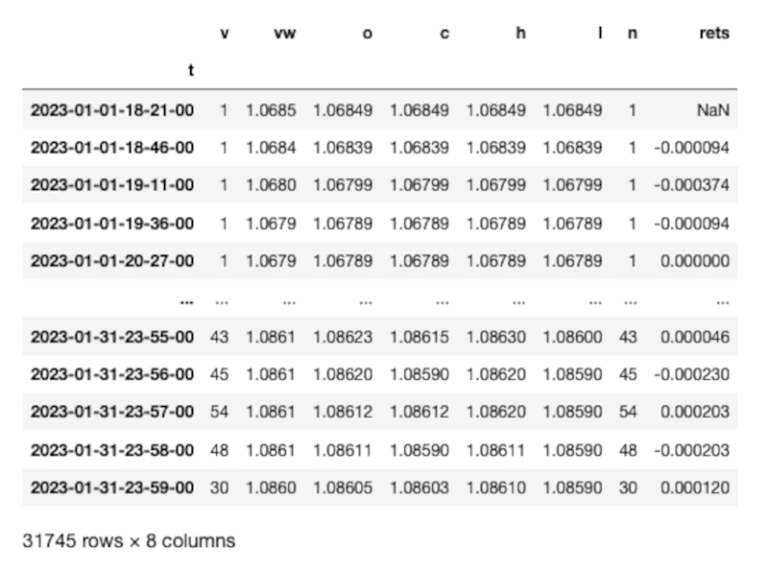
La volatilità realizzata è una misura del rischio. Misura la variabilità di un investimento in un periodo di tempo definito. Viene calcolata come la radice quadrata della somma dei rendimenti al quadrato per uno specifico periodo di tempo. A differenza della volatilità implicita, la volatilità realizzata mostra l’effettiva variazione dei prezzi storici, piuttosto che una previsione della volatilità futura. Tuttavia, è possibile utilizzare i dati per prevedere la volatilità dei rendimenti.
Allora perché è utile? Se riusciamo a prevedere in modo affidabile la volatilità per una finestra temporale futura, è possibile effettuare una valutazione del regime di mercato. Questo può aiutarci a determinare i tipi di strategie di trading che potremmo usare. Ad esempio, nei periodi di bassa volatilità potremmo guardare alle strategie trend-following sulle azioni. In un ambiente ad alta volatilità potremmo prendere in considerazione strategie di mean-reverting o strategie di trading sulle opzioni come Straddle o Strangle. Quantificando il livello di rischio presente nell’universo di trading possiamo prendere decisioni di trading migliori.
Calcolare la volatilità realizzata
La volatilità realizzata è un modo per comprendere il grado di movimento dei prezzi in uno specifico periodo. Per calcolare la volatilità realizzate è necessario:
- Raccogliere i dati sui prezzi e calcolare i rendimenti
- Elevare al quadrato i rendimenti per dare più peso ai cambiamenti più ampi
- Calcolare la media dei rendimenti al quadrato sommandoli e dividendoli per il numero di periodi (noto anche come varianza)
- Prendere la radice quadrata della varianza (nota anche come deviazione standard). Questa è la misura della volatilità realizzata
Infine formiamo un Support Vector Regressor per poter identificare il cambiamento del regime di mercato. A tale scopo dobbiamo calcolare la volatilità realizzata in uno specifico intervallo di tempo. La finestra selezionata dipende dalla frequenza dei dati e dalla liquidità dell’asset. Dato che stiamo considerando sia una coppia FX maggiore che una minore, calcoliamo la volatilità realizzata su 30 punti dati. La libreria Pandas contiene una funzione di rotazione che può essere applicata a qualsiasi aggregatore statistico utilizzando il concatenamento di metodi. In questo caso usiamo rolling() con std(), per calcolare la deviazione standard mobile. La dimensione della finestra mobile può essere impostata su un numero qualsiasi di osservazioni fisse o un delta temporali, ad esempio i giorni lavorativi.
Il codice
Il seguente codice crea una nuova colonna in ciascuno dei DataFrames delle coppie fx che contiene la volatilità realizzata calcolata come deviazione standard mobile degli ultimi 30 punti dati. Questo equivale approssimativamente agli ultimi 30 minuti di dati, con qualche variazione a seconda della frequenza di trading della coppia FX. Diamo un’occhiata alla volatilità realizzata su un grafico.
def create_realised_vol(pairs_rets_dict):
for pair in pairs_rets_dict:
pairs_rets_dict[pair]['realised_vol'] = pairs_rets_dict[pair]['rets'].rolling(30).std()
return pairs_rets_dict
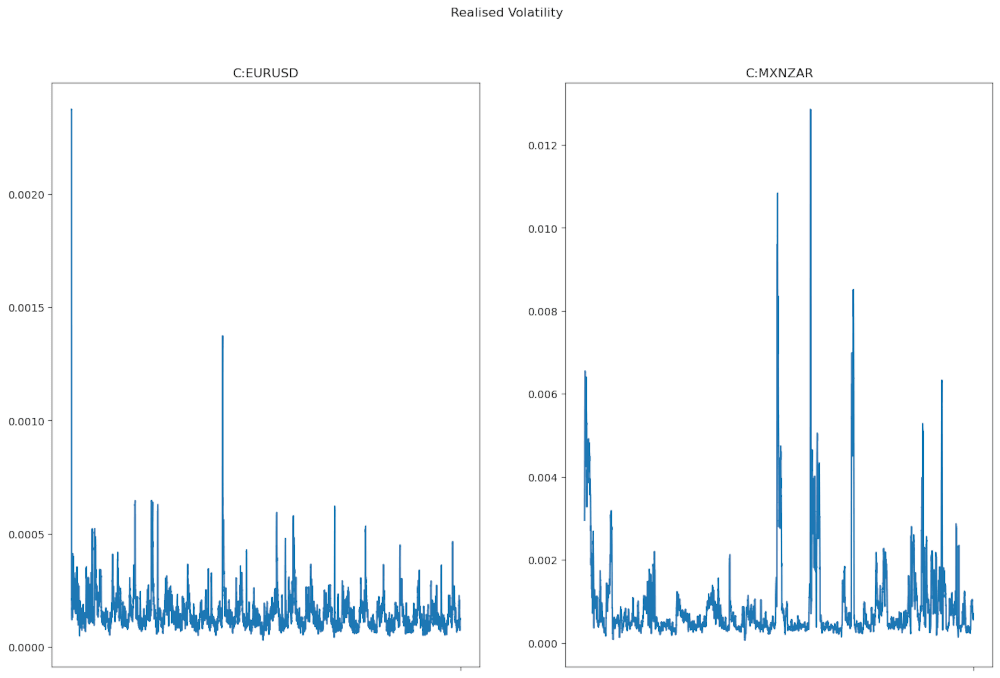
Come possiamo vedere, la coppia esotica MXNZAR ha meno punti dati rispetto a EURUSD, dato che è poco scambiata. Infatti, se osserviamo la lunghezza di entrambi i DataFrames, possiamo vedere che EURUSD ha 31745 righe, mentre MXNZAR ha 16865 righe, quasi la metà. Nell’articolo precedente abbiamo discusso le diverse opzioni a nostra disposizione che permettono di gestire i punti dati mancanti nella coppia MXNZAR.
Esplorare le caratteristiche dei dati
Prima di iniziare a costruire un modello di machine learning è una buona idea dare un’occhiata ai dati e capire come le loro caratteristiche potrebbero influenzare le prestazioni del modello. Perché dovremmo farlo, perché non possiamo semplicemente andare avanti? Bene, in primo luogo la distribuzione dei dati dovrebbe influenzare la scelta del modello. Ad esempio, se i dati fossero distribuiti linearmente, sarebbe appropriato l’uso del modello di regressione lineare o di un kernel lineare in una SVM. Se i dati non sono lineari, sarebbe più appropriato un nucleo di regressione polinomiale o di funzione a base radiale. Potremmo anche prendere in considerazione la trasformazione o il ridimensionamento dei dati per renderli più compatibile con il modello scelto. Verificare se i dati contengono valori anomali o dati mancanti di cui dobbiamo essere a conoscenza. Potrebbe esserci una correlazione (o associazione lineare) tra le caratteristiche selezionate per addestrare il modello. Esistono molti motivi perchè dobbiamo conoscere i propri dati prima di iniziare ad addestrare un modello. In effetti, si stima che tra il 70 e l’80% del tempo di un ingegnere lo trascorra lavorando con i dati. Diamo un’occhiata a una semplice analisi esplorativa dei dati.
Per prima cosa esaminiamo la distribuzione dei rendimenti per entrambe le coppie FX. Usiamo la funzione kdeplot() di Seaborn per visualizzare le distribuzioni.
fig, ax = plt.subplots(2,2, figsize=(16, 10), squeeze=False)
y_data = ['rets', 'realised_vol']
for idx, fxpair in enumerate(fx_pairs_str_ind.keys()):
for idx2, dfcol in enumerate(y_data):
row = (idx)
col = (idx2%2)
sns.kdeplot(fx_pairs_str_ind[fxpair][dfcol], ax=ax[row][col], bw_adjust=0.5)
ax[row][col].set_title(fxpair)
fig.suptitle("KDE of Returns & Realised Volatility")
plt.show()
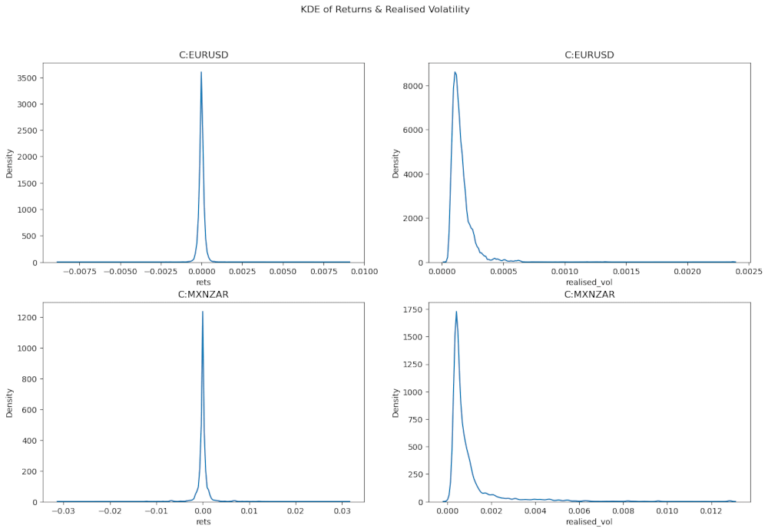
Innanzitutto è importante notare che la scala sull’asse x è diversa tra EURUSD e MXNZAR. La gamma di rendimenti è più ampia per MXNZAR rispetto a EURUSD, sia nella direzione positiva che negativa. Ciò si riflette nella volatilità realizzata. Possiamo anche vedere che abbiamo una curtosi positiva per tutte le distribuzioni rispetto a una distribuzione normale standard. Anche la volatilità realizzata ha un’inclinazione positiva. Queste informazioni saranno utili quando proveremo a scegliere o migliorare i modelli di apprendimento automatico che potremmo voler utilizzare. Infine, nell’esotica coppia FX MXNZAR, possiamo vedere due piccole gobbe appena prima di -0,01 e 0,01. Ciò indica la presenza di picchi nei dati sui rendimenti.
Il grafico a violino
Per esaminarli con maggiore dettaglio possiamo utilizzare il grafico a violino. Questo ci permette di vedere quanti casi di questi picchi ci sono nei nostri dati e quanto sono lontani dalla maggior parte della distribuzione. Il codice seguente crea questo tipo d grafico.
fig, ax = plt.subplots(2,2, figsize=(16, 10), squeeze=False)
y_data = ['rets', 'realised_vol']
for idx, fxpair in enumerate(fx_pairs_str_ind.keys()):
for idx2, dfcol in enumerate(y_data):
row = (idx)
col = (idx2%2)
sns.kdeplot(fx_pairs_str_ind[fxpair][dfcol], ax=ax[row][col], bw_adjust=0.5)
ax[row][col].set_title(fxpair)
fig.suptitle("KDE of Returns & Realised Volatility")
plt.show()
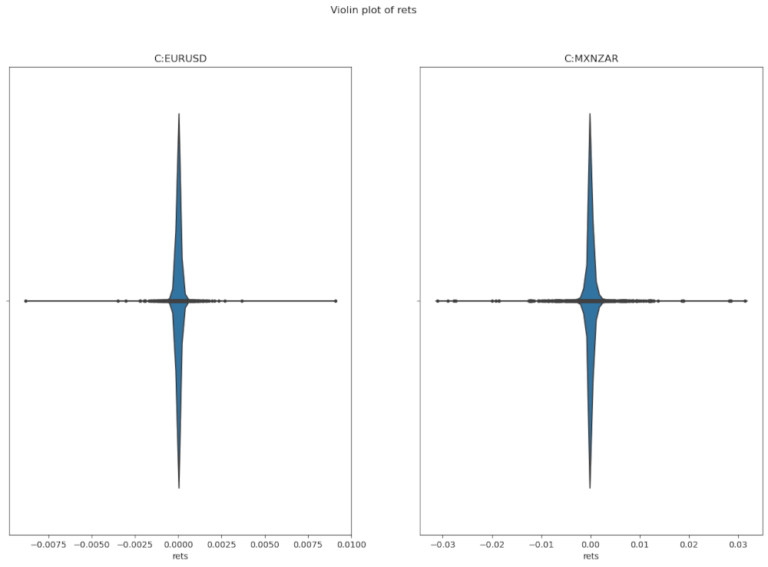
Vediamo che nella coppia FX MXNZAR ci sono più punti più lontani dalla maggior parte della distribuzione. Ciò significa che ci sono più occasioni in cui si verifica un rendimento più alto o più basso rispetto all’EURUSD. Questa informazione da sola potrebbe essere utile quando si considera le strategie di trading.
Modello di machine learning
Poiché stiamo pianificando di inserire i nostri dati in un modello di apprendimento automatico, dobbiamo anche pensare alla correlazione. Vogliamo utilizzare la volatilità realizzata e i rendimenti come caratteristiche in un set di addestramento per un Support Vector Regressor. Dobbiamo assicurarci che queste due caratteristiche non siano correlate, altrimenti forniamo al modello di machine learning le stesse informazioni due volte. Il modello diventerebbe eccessivamente specifico, il che potrebbe portare a scarse prestazioni del modello. Di seguito esaminiamo la correlazione tra le due caratteristiche scelte. Per utilizzare entrambe le feature dovremmo cercare una correlazione prossima allo zero.
La seguente funzione visualizza un grafico a dispersione della serie dei rendimenti e della serie della volatilità realizzata. Utilizza anche il metodo pd.DataFrame.corr di Pandas per calcolare la correlazione tra i due.
fig, ax = plt.subplots(1,2, figsize=(16, 10), squeeze=False)
for idx, fxpair in enumerate(fx_pairs_str_ind.keys()):
row = (idx//2)
col = (idx%2)
print(f"vol and rets correlation for {fxpair} is "
f"{fx_pairs_str_ind[fxpair]['rets'].corr(fx_pairs_str_ind[fxpair]['realised_vol'])}")
sns.scatterplot(data=fx_pairs_str_ind[fxpair], x='rets', y='realised_vol', ax=ax[row][col])
ax[row][col].set_title(fxpair)
fig.suptitle("Correlation between realised vol and returns")
plt.show()
vol and rets correlation for C:EURUSD is 0.008572524273933109
vol and rets correlation for C:MXNZAR is 0.018750753882674935
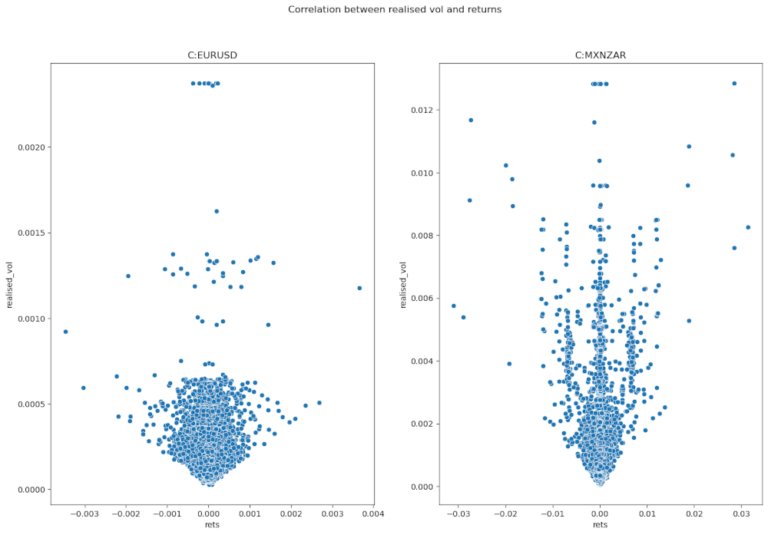
Ora che sappiamo che la serie dei rendimenti e la serie della volatilità realizzata hanno poca correlazione, possiamo usarli come feature separate nel modello di apprendimento automatico.
Conclusione
In questo articolo abbiamo visto come calcolare la volatilità realizzata con i dati Forex di Polygon. Nel prossimo articolo descriviamo come costruire un Support Vector Regressor per determinare l’affidabilità con cui possiamo prevedere il prossimo valore della volatilità realizzata usando i valori dei rendimenti e della volatilità realizzata dei dati precedenti. In questo modo possiamo preparare una pipeline per i nostri dati, comprendere alcuni parametri del modello e prepararci per la specifica finale del modello.