Nell’articolo precedente abbiamo definito l’analisi delle serie temporali come mezzo per aiutarci a creare strategie di trading. In questo articolo esamineremo uno degli aspetti più importanti delle serie temporali, ovvero la correlazione seriale (nota anche come autocorrelazione).
Prima di immergerci nella definizione di correlazione seriale, discuteremo l’ampio scopo della modellazione di serie temporali e perché siamo interessati alla correlazione seriale.
Quando ci vengono fornite una o più serie temporali finanziarie, siamo principalmente interessati alla previsione o alla simulazione dei dati. È relativamente semplice identificare trend deterministiche e anche variazioni stagionali, oltre che scomporre una serie in queste componenti. Tuttavia, una volta scomposta una serie temporale in questo modo, resta esclusa una componente casuale.
A volte una serie temporale di questo tipo può essere ben modellata da variabili casuali indipendenti. Tuttavia, vi sono molte situazioni, in particolare nella finanza, in cui elementi consecutivi di questa serie temporale di componenti casuali avranno una correlazione . Cioè, il comportamento dei punti sequenziali nelle serie rimanenti si influenzano a vicenda in modo dipendente. Un esempio importante si verifica nel trading di coppie con ritorno alla media. Il ritorno alla media si presenta come correlazione tra variabili sequenziali nelle serie temporali.
Il nostro compito come modellatori quantitativi è cercare di identificare la struttura di queste correlazioni, in quanto ci consentiranno di migliorare notevolmente le nostre previsioni e quindi la potenziale redditività di una strategia. Inoltre, l’identificazione della struttura di correlazione migliorerà il realismo di qualsiasi serie temporale simulata basata su tale modello. Ciò è estremamente utile per migliorare l’efficacia delle componenti di gestione del rischio nell’attuazione della strategia.
Quando le osservazioni sequenziali di una serie temporale sono correlate nel modo descritto sopra, diciamo che esiste una correlazione seriale (o autocorrelazione) nelle serie temporali.
Ora che abbiamo delineato l’utilità dello studio della correlazione seriale, dobbiamo definirla in modo rigorosamente matematico. Prima di poterlo fare, dobbiamo introdurre concetti più semplici, incluse l’aspettativa e la varianza.
Aspettativa, varianza e covarianza
Molte di queste definizioni risulteranno familiari alla maggior parte dei lettori di DataTrading, ma le descriverò specificamente per motivi di completezza.
La prima definizione è quella del valore atteso o aspettativa :
Aspettativa
Il valore atteso o aspettativa, \(E(x)\), di una variabile casuale \(x\) è il suo valore medio nella popolazione. Indichiamo l’aspettativa di \(x\) con \(\mu\), in modo tale che \(E(x) = \mu \).
Ora che abbiamo la definizione di aspettativa possiamo definire la varianza , che caratterizza lo “spread” di una variabile casuale:
Varianza
La varianza di una variabile casuale è l’aspettativa delle deviazioni al quadrato della variabile dalla media, indicata con \(\sigma^2(x) = E[(x-\mu)^2] \).
Notare che la varianza è sempre non negativa. Questo ci permette di definire la deviazione standard :
Deviazione standard
La deviazione standard di una variabile casuale \(x\), \(\sigma(x) \), è la radice quadrata della varianza di \(x\).
Ora che abbiamo delineato queste definizioni statistiche elementari, possiamo generalizzare la varianza al concetto di covarianza tra due variabili casuali. La covarianza ci dice quanto linearmente siano correlate queste due variabili:
Covarianza
La covarianza di due variabili casuali \(x\) e \(y\), ciascuna con le rispettive aspettative \(\mu_x\) e \(\mu_y\), è data da \(\sigma(x, y) = E [(x-\mu_x) (y – \mu_y)]\).
La covarianza ci dice come due variabili si muovono insieme.
Tuttavia, poiché siamo in una situazione statistica, non abbiamo accesso alla popolazione significa \(\mu_x\) e \(\mu_y\). Invece dobbiamo stimare la covarianza da un campione . Per questo usiamo il rispettivo campione significa \(\bar{x}\) e \(\bar{y}\).
Se consideriamo un insieme di \(n\) coppie di elementi di variabili casuali da \(x\) e \(y\), dato da \((x_i, y_i)\), la covarianza campionaria , \(\text{Cov}(x, y)\) (anche a volte indicato con \(q(x, y)\)) è dato da:
\(\begin{eqnarray} \text {Cov} (x, y) = \frac {1} {n-1} \sum ^ n_ {i = 1} (x_i – \bar {x}) (y_i – \bar { y}) \end{eqnarray}\)
Nota: alcuni di voi potrebbero chiedersi perché dividiamo per \(n-1\) al denominatore, invece che per \(n\). Questa è una domanda valida! E’ opportuno scegliere \(n-1\) in moda da rendere \(\text {Cov} (x, y)\) un Bias di Stima.
Esempio: Covarianza campionaria in Python
Per calcolare la covarianza possiamo utilizzare la libreria Numpy di Python. NumPy non ha una funzione per calcolare direttamente la covarianza tra due variabili, ma prevede una funzione per calcolare una matrice di covarianza chiamata cov() che possiamo usare per recuperare la covarianza. Come default, la funzione cov() calcolerà la covarianza campionaria tra le variabili casuali in input.
Nel seguente codice simuleremo due vettori di lunghezza 100, ciascuno con una sequenza di numeri interi crescente linearmente con l’aggiunta di rumore normalmente distribuito. Quindi stiamo costruendo variabili associate linearmente in base alla progettazione .
Per prima cosa costruiremo un grafico a dispersione e quindi calcoleremo la covarianza del campione utilizzando la funzione cov(). Per assicurarsi di lavorare esattamente gli stessi dati di seguito utilizzati, si imposta un seed casuale rispettivamente di 1 e 2 per ogni variabile:
np.random.seed(1)
x = np.arange(100) + 20 * np.random.normal(size=100)
np.random.seed(2)
y = np.arange(100) + 20 * np.random.normal(size=100)
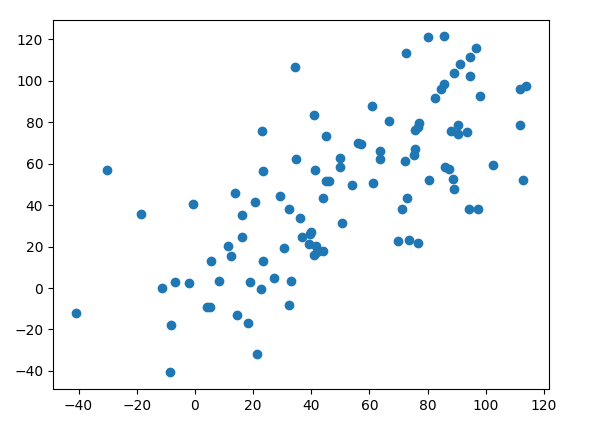
Esiste un’associazione relativamente chiara tra le due variabili.
Possiamo ora calcolare la covarianza per le due variabili come l’elemento [0,1] della matrice di covarianza quadrata:
sigma = np.cov(x,y)[0,1]
print(sigma)
La covarianza campionaria è pari a 926,1397…
Uno svantaggio dell’utilizzo della covarianza per stimare l’associazione lineare tra due variabili casuali è che la covarianza è una misura dimensionale . Cioè, non è normalizzato dalla diffusione dei dati e quindi è difficile fare confronti tra set di dati con grandi differenze di diffusione. Questo motiva l’introduzione di un altro concetto, vale a dire la correlazione.
Correlazione
La correlazione è una misura adimensionale della relazione tra due variabili tale che a ciascun valore della prima corrisponda un valore della seconda, seguendo una certa regolarità. In sostanza, è la covarianza di due variabili casuali, normalizzate con i rispettivi spread. La correlazione tra due variabili è spesso indicata con \(\rho(x, y)\):
\(\begin{eqnarray} \rho(x,y) = \frac {E[(x-\mu_x) (y-\mu_y)]} {\sigma_x \sigma_y} = \frac {\sigma(x,y)} {\sigma_x \sigma_y} \end{eqnarray}\)
Il prodotto dei due spread al denominatore vincola la correlazione ad assumere valori nell’intervallo \([-1,1]\):
- Una correlazione di \(\rho(x, y) = +1\) indica un’esatta relazione lineare positiva
- Una correlazione di \(\rho(x, y) = 0\) indica nessuna relazione lineare
- Una correlazione di \(\rho(x, y) = -1\) indica un’esatta relazione lineare negativa
Come per la covarianza, possiamo definire la correlazione campionaria, \(\text{Cor}(x, y)\) come:
\(\begin{eqnarray} \text{Cor} (x, y) = \frac {\text{Cov (x, y)}} {\text {sd}(x) \text{sd} (y)} \end{eqnarray}\)
Dove \(\text{Cov} (x, y) \) è la covarianza campionaria di \(x\) e \(y\), mentre \(\text{sd}(x)\) è la deviazione standard campionaria di \(x\).
Esempio: correlazione campionaria in Python
NumPy fornisce la funzione corrcoef() per calcolare direttamente la correlazione tra due variabili. Come cov(), restituisce una matrice, in questo caso una matrice di correlazione, e possiamo accedere alla correlazione che ci interessa tramite il valore [0,1] della matrice quadrata restituita.
Usando gli stessi vettori \(x\) e \(y\) dell’esempio precedente, il seguente codice Python calcola la correlazione campionaria:
corr = np.corrcoef(x,y)[0,1]
print(corr)
La correlazione del campione è fornita come 0,69839 che mostra un’associazione lineare positiva ragionevolmente forte tra i due vettori, come previsto.
Stazionarietà nelle serie storiche
Ora che abbiamo delineato le definizioni generali di aspettativa, varianza, deviazione standard, covarianza e correlazione, possiamo descrivere come applicare questi concetti ai dati delle serie temporali.
In primo luogo, introduciamo un concetto noto come stazionarietà. Questo è un aspetto estremamente importante delle serie temporali e gran parte dell’analisi effettuata sui dati delle serie temporali finanziarie riguarderà la stazionarietà. Dopo aver discusso la stazionarietà, siamo in grado di parlare di correlazione seriale e costruire alcuni grafici di correlogramma.
Iniziamo cercando di applicare le definizioni di cui sopra ai dati di serie temporali, partendo dalla media / aspettativa:
Media di una serie storica
La media di una serie temporale \( x_t \), \( \mu(t) \), corrispondete all’aspettativa \( E(x_t) = \mu(t)\).
In questa definizione ci sono due punti importanti da sottolineare:
- \( \mu = \mu(t)\), cioè la media (in generale) è una funzione del tempo.
- Questa aspettativa viene ricavata dall’insieme della popolazione di tutte le possibili serie temporali che possono essere generate con il modello delle serie temporali. In particolare, NON corrispondere all’espressione \( (x_1 + x_2 + … + x_k) / k \) (descritta più avanti).
Questa definizione è utile quando siamo in grado di generare molte realizzazioni di un modello di serie temporale. Tuttavia questo non è possibile nella realtà: siamo “bloccati” con una sola storia passata e quindi abbiamo, quasi sempre, accesso solo a una singola serie storica per una particolare risorsa o situazione.
Quindi come si procede se si vuole stimare la media, dato che non abbiamo accesso a queste ipotetiche realizzazioni dall’insieme? Bene, ci sono due opzioni:
- Stima semplicemente la media in ogni punto utilizzando il valore osservato.
- Scomporre le serie temporali per rimuovere eventuali tendenze deterministiche o effetti di stagionalità, ottenendo una serie residua . Una volta ottenuta questa serie possiamo ipotizzare che la serie residua sia stazionaria nella media , cioè che \( \mu (t) = \mu \), un valore fisso indipendente dal tempo. Diventa quindi possibile stimare questa media costante della popolazione utilizzando la media campionaria \( \bar {x} = \sum ^ {n}_{t = 1} \frac {x_t} {n} \).
Stazionarietà della Media
Una serie temporale è media-stazionaria se \( \mu(t) = \ mu \), cioè è costante nel tempo.
Ora che abbiamo visto come possiamo descrivere i valori delle aspettative, possiamo usarli per arricchire la definizione di varianza. Ancora una volta facciamo l’ipotesi semplificativa che la serie temporale in esame ha media stazionaria. Con questo assunto possiamo definire la varianza come:
Varianza di una serie storica
La varianza \( \sigma ^ 2 (t) \) di un modello di serie temporale con media stazionaria è data da \( \sigma ^ 2 (t) = E [(x_t – \mu) ^ 2] \).
Questa è una semplice estensione della varianza definita in precedenza per le variabili casuali, tranne per il fatto che \(\ sigma ^ 2 (t) \) è una funzione del tempo. È importante notare come la definizione si basi fortemente sul fatto che la serie temporale ha una media stazionaria (cioè che \(\mu \) non è dipendente dal tempo).
Si può notare che questa definizione porta a una situazione complicata. Se la varianza stessa varia nel tempo, come possiamo stimarla da una singola serie temporale? Come prima, la presenza di \( E (..) \) richiede un insieme di serie temporali e tuttavia spesso ne abbiamo solo una!
Ancora una volta, semplifichiamo la situazione facendo un’ipotesi. In particolare, come per la media, assumiamo una varianza costante della popolazione, indicata con \( \sigma ^ 2 \), che non è funzione del tempo. Una volta fatta questa ipotesi, siamo in grado di stimarne il valore utilizzando la definizione di varianza campionaria introdotta in precedenza:
\(\begin{eqnarray} \text {Var (x)} = \frac {\sum (x_t – \ bar {x}) ^ 2} {n-1} \end{eqnarray}\)
Affinché questo funzioni dobbiamo essere in grado di stimare la media campionaria, \( \bar {x} \). Inoltre, come per la covarianza campionaria definita sopra, dobbiamo usare \( n-1 \) al denominatore per rendere la varianza campionaria uno stimatore imparziale.
Stazionarietà della varianza
Una serie temporale è stazionaria nella varianza se \( \ sigma ^ 2 (t) = \ sigma ^ 2 \), è costante nel tempo.
È qui che dobbiamo stare attenti! Con le serie temporali ci troviamo nella situazione dove le osservazioni sequenziali possono essere correlate. Questo può influenzare lo stimatore, ovvero sovrastimare o sottovalutare la reale varianza della popolazione.
Ciò sarà particolarmente problematico nelle serie temporali di cui abbiamo pochi dati e quindi abbiamo solo un piccolo numero di osservazioni. In una serie ad alta correlazione, tali osservazioni saranno vicine l’una all’altra e quindi introduco un bias .
In pratica, e in particolare nella finanza ad alta frequenza, ci troviamo spesso nella situazione di avere un numero considerevole di osservazioni. Lo svantaggio è che spesso non possiamo presumere che le serie finanziarie siano veramente stazionarie nella media o stazionarie nella varianza .
Man mano che progrediamo con questa serie di articoli e sviluppiamo modelli più sofisticati, affronteremo questi problemi al fine di migliorare le nostre previsioni e simulazioni.
Siamo ora in grado di applicare le nostre definizioni di serie temporali di media e varianza a quella di correlazione seriale.
Correlazione seriale
Infine, siamo in grado di definire la covarianza seriale e la correlazione seriale!Stazionarietà di secondo ordine Una serie temporale è stazionaria di secondo ordine se la correlazione tra le osservazioni sequenziali è una funzione solamente del ritardo (lag), cioè il numero di periodi temporali che separa ciascuna osservazione sequenziale.
L’autocovarianza \(C_k\) non è una funzione del tempo perché implica un’aspettativa \(E(..)\), che, come visto in precedenza, viene presa dall’insieme della popolazione delle possibili serie temporali. Ciò significa che è costante per tutti i valori di \(t\). Da cui si ricava la definizione di correlazione seriale o autocorrelazione semplicemente dividendo per il quadrato della diffusione della serie. Questo è possibile perché la serie temporale è stazionaria nella varianza e quindi \( \sigma^2(t) = \sigma^ 2 \):Autocovarianza di una serie storica Se un modello di serie temporale è stazionario di secondo ordine, allora la covarianza seriale o autocovarianza , di ritardo \( k \), è definita come: \(C_k = E [(x_t- \mu) (x_ {t + k} – \mu)] \).
Da notare che \( \rho_0 = \frac{C_0} {\sigma^2} = \frac{E [(x_t – \mu) ^ 2]} {\sigma ^ 2} = \frac {\sigma ^ 2} {\sigma ^ 2} = 1 \). Cioè, il primo ritardo di \( k = 0 \) darà sempre un valore unitario. Come con le definizioni precedenti di covarianza e correlazione, possiamo definire l’autocovarianza e l’autocorrelazione campionarie. In particolare, denotiamo l’autocovarianza campionaria con \(c\) minuscola per differenziare il valore della popolazione dato dalla \( C \) maiuscola. La funzione di autocovarianza di esempio \( c_k \) è data da:Autocorrelazione di una serie storica La correlazione seriale o autocorrelazione del ritardo \(k\), \(\rho_k\), di una serie temporale stazionaria di secondo ordine è data dall’autocovarianza della serie normalizzata dal prodotto dello spread. Cioè \(\rho_k = \frac {C_k} {\sigma^2} \).
\(\begin{eqnarray} c_k = \ frac {1} {n} \ sum ^ {nk} _ {t = 1} (x_t – \ bar {x}) (x_ {t + k} – \ bar {x}) \end{eqnarray}\)
La funzione di autocorrelazione di esempio \(r_k\) è data da:\(\begin{eqnarray} r_k = \ frac {c_k} {c_0} \end{eqnarray}\)
Ora che abbiamo definito la funzione di autocorrelazione campionaria siamo in grado di definire e tracciare il correlogramma , strumento essenziale nell’analisi delle serie temporali.Il Correlogramma
Un correlogramma è semplicemente un grafico della funzione di autocorrelazione per valori sequenziali del ritardo, \( k = 0,1, …, n \). Ci permette di vedere la struttura di correlazione in ogni lag.
L’utilizzo principale dei correlogrammi è quello di rilevare eventuali autocorrelazioni successive alla rimozione di trend deterministici e effetti di stagionalità.
Se abbiamo adattato un modello di serie temporale, il correlogramma ci aiuta a giustificare che questo modello è ben adattato o se è necessario perfezionarlo ulteriormente per rimuovere qualsiasi autocorrelazione aggiuntiva.
Ecco un esempio di correlogramma, graficato tramite Python utilizzando la funzione acf, per una sequenza di variabili casuali normalmente distribuite. Di seguito potete trovare il codice Python completo:
from statsmodels.graphics.tsaplots import plot_acf
from statsmodels.tsa.stattools import acf
import matplotlib.pyplot as plt
import numpy as np
np.random.seed(1)
s = np.random.normal(size=100)
acf_coef = acf(s)
plot_acf(acf_coef, lags=20)
plt.show()
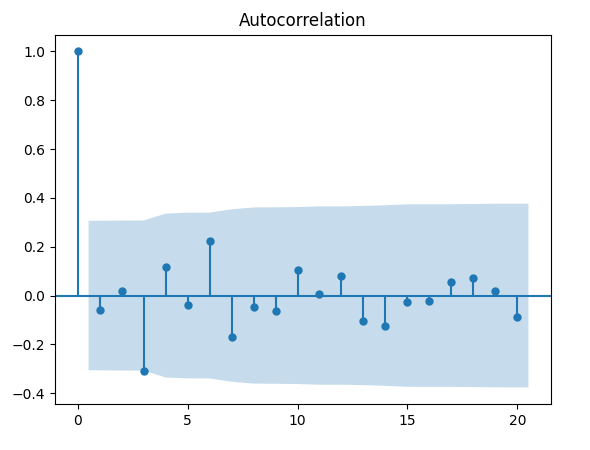
Da notare le caratteristiche specifiche del grafico del correlogramma:
- In primo luogo, poiché la correlazione campionaria del ritardo \( k = 0 \) è data da \( r_0 = \frac {c_0} {c_0} = 1 \), nel grafico avremo sempre una linea di altezza uguale ad 1 per il ritardo \( k = 0 \). In effetti, questo ci fornisce un punto di riferimento su cui giudicare le restanti autocorrelazioni per i ritardi successivi. Si noti inoltre che l’ACF dell’asse y è adimensionale, poiché la correlazione è essa stessa adimensionale.
- L’area blu rappresenta il confine per cui se i valori non rientrano in questa area, si ha evidenza che la nostra correlazione al lag \( k \), \( r_k \), sia uguale a zero al livello del 5%. Tuttavia dobbiamo fare attenzione perché dovremmo aspettarci che il 5% di questi ritardi superi comunque questi valori! Inoltre stiamo visualizzando i valori correlati e quindi se un ritardo cade al di fuori di questi limiti, è più probabile che lo facciano anche i prossimi valori sequenziali. In pratica stiamo cercando ritardi che possano avere qualche motivo di fondo per superare il livello del 5%. Ad esempio, in una serie temporale di materie prime potremmo vedere effetti imprevisti della stagionalità a determinati ritardi (possibilmente intervalli mensili, trimestrali o annuali).
Ecco un paio di esempi di correlogrammi per sequenze di dati.
Esempio 1 – Trend lineare fisso
Il seguente codice Python genera una sequenza di numeri interi da 1 a 100 e quindi traccia l’autocorrelazione:
w = np.arange(1, 100)
acf_coef = acf(w, nlags=100)
plot_acf(acf_coef, lags=20)
plt.show()
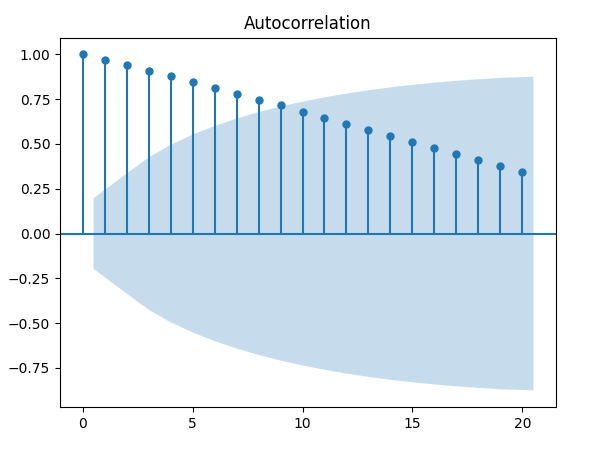
Da notare come il grafico ACF diminuisce in modo quasi lineare all’aumentare dei ritardi. Quindi un correlogramma di questo tipo è una chiara indicazione della presenza di un trend.
Esempio 2 – Sequenza ripetuta
Il seguente codice Python genera una sequenza ripetuta di numeri con periodo \( p = 10 \) e quindi traccia l’autocorrelazione:
a = np.arange(1,11)
s = []
for i in range (0,10):
for j in range (0,10):
s.append(a[j])
acf_coef = acf(s)
plot_acf(acf_coef, lags=20)
plt.show()
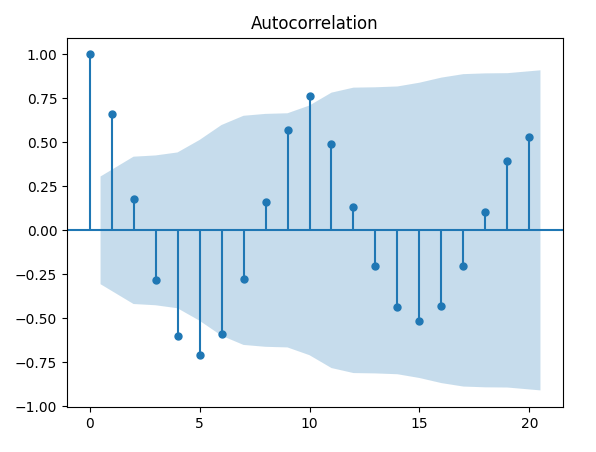
Possiamo vedere che ci sono picchi significativi per i ritardi 10 e 20. Ciò ha senso, poiché le sequenze si ripetono con un periodo di 10. È interessante notare che esiste una correlazione negativa esattamente del -0,5 per i ritardi 5 e 15. Questo è molto caratteristico delle serie temporali stagionali e un comportamento di questo tipo in un correlogramma è solitamente indicativo che la stagionalità / effetti periodici non sono stati completamente considerati nel modello.
Prossimi passi
Ora che abbiamo descritto in modo approfondito l’autocorrelazione e i correlogrammi, nei prossimi articoli passeremo ai modelli lineari e inizieremo il processo di previsione .
Sebbene i modelli lineari siano lontani dallo stato dell’arte nell’analisi delle serie temporali, dobbiamo sviluppare la teoria su casi più semplici prima di poterla applicare ai modelli non lineari più interessanti che sono oggi in uso.