Una tecnica di quant trading prevede di considerare due asset che hanno una relazione di cointegrazione e l’utilizzo di un approccio mean-reverting per costruire una strategia di trading. Questo può essere effettuato eseguendo una regressione lineare tra i due asset (come una coppia di ETF) e utilizzare la regressione per determinare la quantità di ciascuna asset per andare long e short con determinate soglie.
Una delle principali criticità di tale strategia è la variazione nel tempo di qualsiasi parametro introdotto attraverso questa relazione strutturale, come il rapporto di copertura tra i due asset. Cioè, i parametri non sono fissi durante tutto il periodo di attività della strategia. Al fine di migliorare la redditività è utile poter disporre di un meccanismo di aggiustamento del rapporto di copertura nel tempo.
Per risolvere questo problema si può utilizzare una regressione lineare mobile in una finestra di ricerca (o periodo temporale), cioè è necessario aggiornare la regressione lineare ad ogni nuova barra in modo che i termini di pendenza e di intercetta “seguano” l’ultimo valore osservato della relazione di cointegrazione. Tuttavia, in questo modo si introduce nella strategia un altro parametro variabile, ovvero la lunghezza della finestra di ricerca. Questo parametro deve essere ottimizzato, ad esempio tramite la convalida incrociata .
Un approccio più sofisticato consiste nell’utilizzare un modello dello spazio degli stati, dove si considera il “vero” rapporto di copertura come una variabile nascosta non osservata e tenta di stimarlo con osservazioni “rumorose”, cioè i dati dei prezzi di ogni asset.
Il filtro Kalman esegue esattamente questo compito. In un articolo precedente abbiamo descritto in modo approfondito il filtro di Kalman e la sua applicazione come un processo di aggiornamento bayesiano.
In questo articolo usiamo il filtro Kalman, tramite la libreria pykalman di Python, per aiutarci a stimare dinamicamente la pendenza e l’intercettazione (e quindi il rapporto di copertura) tra una coppia di ETF.
Questa tecnica è infine testata con il sistema di trading DataTrader, che ci consente di verificare le prestazioni di una questa strategia negli ultimi anni.
Breve riepilogo del filtro di Kalman
Per capire le basi matematiche si può leggere l’articolo precedente, dove le formule del Filtro di Kalman sono descritte in modo approfondito. Di seguito riassumiamo brevemente i punti chiave qui.
In questo caso usiamo un modello dello spazio degli stati composto da due equazioni matriciali. La prima è nota come equazione di stato o di transizione e descrive come un insieme di variabili di stato,\(\theta_t\), vengono modificati da un periodo di tempo all’altro. La dipendenza lineare dallo stato precedente è rappresentata da matrice di transizione \(G_t\) e dal rumore di sistema normalmente distribuito \(w_t\). Da notare che \(G=G_t\) , cioè la matrice di transizione è essa stessa dipendente dal tempo:
\(\begin{eqnarray}\theta_t = G_t \theta_{t-1} + w_t\end{eqnarray}\)
Tuttavia, questi stati sono spesso non osservabili ed ogni intervallo di tempo potremmo avere accesso solo alle osservazioni, descritte da \(y_t\). Le osservazioni sono associate ad un’equazione di osservazione che include una componente lineare tramite la matrice di osservazione \(F_t\), oltre ad un rumore di misura normalmente distribuito dato da \(v_t\).
\(\begin{eqnarray}y_t = F_t \theta_t + v_t \end{eqnarray}\)
Per maggiori dettagli sul modello dello spazio degli stati e sul filtro di Kalman, fare riferimento al precedente articolo .
Incorporare la regressione lineare in un filtro di Kalman
La domanda principale in questa fase è come utilizziamo questo modello dello spazio degli stati per incorporare le informazioni in una regressione lineare?
Come descritto nell’articolo sul MLE per la regressione lineare, una regressione lineare multipla prevede che il valore in uscita \(y\) è una funzione lineare delle componenti in input \(x\):
\(\begin{eqnarray}y({\bf x}) = \beta^T {\bf x} + \epsilon\end{eqnarray}\)
dove \(\beta^T = (\beta_0, \beta_1, \ldots, \beta_p)\) rappresenta il vettore di trasposizione dell’intercetta \(\beta_0\) e pendenze \(\beta_i\), insieme a \(\epsilon \sim \mathcal{N}(\mu, \sigma^2)\) che rappresenta il termine di errore.
Poiché siamo in un ambiente unidimensionale, possiamo semplicemente scrivere \(\beta^T = (\beta_0, \beta_1)\) e \({\bf x} = \begin{pmatrix} 1 \\ x \end{pmatrix}\).
Consideriamo gli stati (nascosti) del sistema in modo che siano rappresentati dal vettore \(\beta^T\), ovvero l’intercetta e la pendenza della regressione lineare. Il passaggio successivo consiste nell’assumere che l’intercetta e la pendenza di domani siano uguali all’intercetta e alla pendenza di oggi con l’aggiunta di un rumore di sistema casuale. Questo gli conferisce la natura di una passeggiata casuale, il cui comportamento è descritto in dettaglio nell’articolo sul rumore bianco e le passeggiate casuali:
\(\begin{eqnarray}\beta_{t+1} ={\bf I} \beta_{t} + w_t\end{eqnarray}\)
Dove la matrice di transizione è impostata sulla matrice di identificazione bidimensionale, \(G_t = {\bf I}\), che rappresenta la metà del modello dello spazio degli stati. Il passaggio successivo consiste nell’utilizzare effettivamente uno degli ETF della coppia come “osservazioni”.
Applicazione del filtro di Kalman a una coppia di ETF
Per formare l’equazione di osservazione è necessario scegliere una delle serie di prezzi dell’ETF come variabile “osservata”, \(y_t\), e la serie dell’altro ETF come formulazione di regressione lineare \(x_t\) descritta in precedenza:
\(\begin{eqnarray}y_t &=& F_t {\bf x}_t + v_t \\
&=& (\beta_0, \beta_1 ) \begin{pmatrix} 1 \\ x_t \end{pmatrix} + v_t\end{eqnarray}\)
Quindi abbiamo la regressione lineare riformulata come un modello dello spazio degli stati, che ci consente di stimare l’intercetta e la pendenza quando arrivano nuovi dati di prezzo tramite il filtro di Kalman.
TLT ed ETF
Prenderemo in considerazione due ETF a reddito fisso, ovvero iShares 20+ Year Treasury Bond ETF (TLT) e iShares 3-7 Year Treasury Bond ETF (IEI) . Entrambi questi ETF replicano la performance di obbligazioni del Tesoro statunitensi di durata variabile e, in quanto tali, sono entrambi esposti a fattori di mercato simili. Analizziamo il loro comportamento di regressione negli ultimi cinque anni circa.
Grafico a dispersione dei prezzi degli ETF
Usiamo una varietà di librerie Python, tra cui numpy, matplotlib, pandas e pykalman per analizzare il comportamento di una regressione lineare dinamica tra questi due titoli. Come per tutti i programmi Python, il primo compito è importare le librerie necessarie:
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import yfinance as yf
from pykalman import KalmanFilter
Nota: probabilmente dovrai eseguire pip install pykalman per installare la libreria PyKalman.
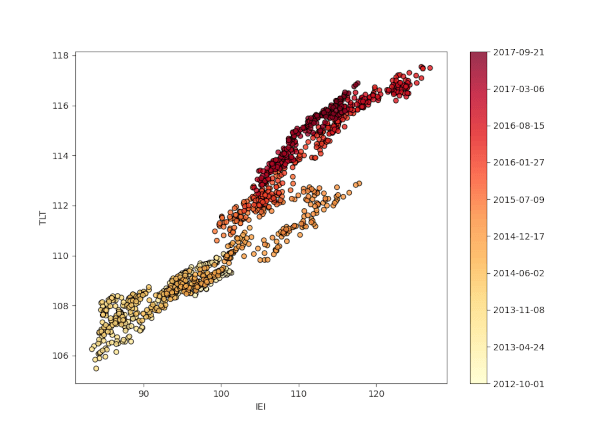
Dobbiamo ora scrivere la funzione draw_date_coloured_scatterplot per produrre un grafico a dispersione dei prezzi di chiusura rettificati dell’asset. Il grafico a dispersione verrà colorato utilizzando la mappa dei colori matplotlib, in particolare “Yellow To Red”, dove il giallo rappresenta le coppie di prezzi più vecchie, mentre il rosso rappresenta le coppie di prezzi più recenti:
def draw_date_coloured_scatterplot(etfs, prices):
"""
Creare un grafico scatterplot dei prezzi di due ETF, che è
colorato dalle date dei prezzi per indicare il cambiamento
della relazione tra le due serie di prezzi
"""
# Creare a una mappa di colore da giallo a rosso dove il giallo
# indica le date più vecchie e il rosso indica le date recenti
# early dates and red indicates later dates
plen = len(prices)
colour_map = plt.cm.get_cmap('YlOrRd')
colours = np.linspace(0.1, 1, plen)
# Creare l'oggetto scatterplot
scatterplot = plt.scatter(
prices[etfs[0]], prices[etfs[1]],
s=30, c=colours, cmap=colour_map,
edgecolor='k', alpha=0.8
)
# Aggiungere una barra di colori per la colorazione dei dati ed
# impostare le etichette dell'asse corrispondente
colourbar = plt.colorbar(scatterplot)
colourbar.ax.set_yticklabels(
[str(p.date()) for p in prices[::plen // 9].index]
)
plt.xlabel(prices.columns[0])
plt.ylabel(prices.columns[1])
plt.show()
Abbiamo commentato il codice, quindi dovrebbe essere abbastanza semplice capire il significato di tutti i comandi. Il lavoro principale viene svolto all’interno delle variabili colour_map, colours e scatterplot. Si ottiene il seguente grafico:
Pendenza e intercetta variabili nel tempo
Il passaggio successivo consiste nell’utilizzare effettivamente pykalman per regolare dinamicamente l’intercetta e la pendenza tra TFT e IEI. Questa funzione è più complessa e richiede alcune spiegazioni.
Per prima cosa definiamo una variabile chiamata delta, che viene utilizzata per controllare la covarianza di transizione per il rumore del sistema. Nell’articolo sulla teoria del filtro Kalman questo era indicato con \(W_t\). Moltiplichiamo semplicemente tale valore per la matrice dell’identità bidimensionale.
Il passaggio successivo consiste nel creare la matrice di osservazione. Come abbiamo descritto in precedenza, questa matrice è un vettore composto dai prezzi di TFT e una sequenza di valori unitari. Per costruirlo utilizziamo il metodo vstack di numpy per impilare verticalmente queste due serie di prezzi in un vettore a colonna singola, che poi trasponiamo.
A questo punto utilizziamo la classe KalmanFilter di pykalman per creare l’istanza del filtro Kalman. Forniamo la dimensione delle osservazioni (unitaria in questo caso), la dimensione degli stati (due in questo caso poiché stiamo osservando l’intercetta e la pendenza della regressione lineare).
Dobbiamo anche fornire la media e la covarianza dello stato iniziale. In questo caso impostiamo la media dello stato iniziale a zero sia per l’intercetta che per la pendenza, mentre prendiamo la matrice di identità bidimensionale per la covarianza dello stato iniziale. Le matrici di transizione sono date anche dalla matrice identità bidimensionale.
Gli ultimi termini da specificare sono le matrici di osservazione in obs_mat, con la sua covarianza uguale all’unità. Infine la matrice di covarianza di transizione (controllata da delta) è data da trans_cov.
Ora che abbiamo l’istanza kf del filtro Kalman, possiamo utilizzarla per filtrare in base ai prezzi rettificati da IEI. Questo ci fornisce la media degli stati dell’intercetta e della pendenza, cioè quello che stiamo cercando. Inoltre ricaviamo anche le covarianze degli stati.
Tutto questo è raccolto nella funzione calc_slope_intercept_kalman:
def calc_slope_intercept_kalman(etfs, prices):
"""
Utilizzo del filtro Kalman dal pacchetto pyKalman
per calcolare la pendenza e l'intercetta della
regressione lineare dei prezzi degli ETF.
"""
delta = 1e-5
trans_cov = delta / (1 - delta) * np.eye(2)
obs_mat = np.vstack(
[prices[etfs[0]], np.ones(prices[etfs[0]].shape)]
).T[:, np.newaxis]
kf = KalmanFilter(
n_dim_obs=1,
n_dim_state=2,
initial_state_mean=np.zeros(2),
initial_state_covariance=np.ones((2, 2)),
transition_matrices=np.eye(2),
observation_matrices=obs_mat,
observation_covariance=1.0,
transition_covariance=trans_cov
)
state_means, state_covs = kf.filter(prices[etfs[1]].values)
return state_means, state_covs
Infine tracciamo il grafico dei valori restituiti dalla funzione precedente. Per raggiungere questo obiettivo, creiamo un DataFrame pandas delle pendenze e intercette per gli intervalli temporali t, utilizzando l’indice del DataFrame prices, e tracciamo ogni colonna come un grafico:
def draw_slope_intercept_changes(prices, state_means):
"""
Tracciare la variazione di pendenza e intercetta
dai valori calcolati dal Filtro di Kalman.
"""
pd.DataFrame(
dict(
slope=state_means[:, 0],
intercept=state_means[:, 1]
), index=prices.index
).plot(subplots=True)
plt.show()
Si ottiene il seguente grafico:
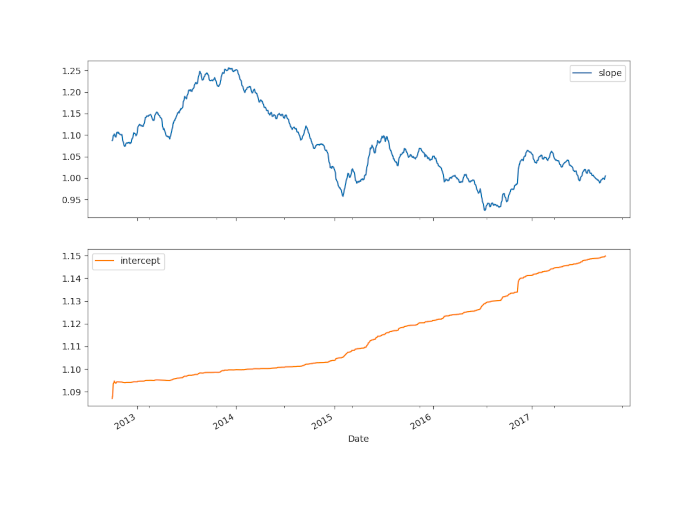
Chiaramente la pendenza variabile nel tempo cambia drasticamente nel periodo, scendendo da circa 1,25 nel 2014 a circa 0,9 nel 2016. Non è difficile vedere che l’utilizzo di un hedge ratio fisso in una strategia di pairs trading sarebbe troppo rigido.
Inoltre la stima della pendenza subisce l’effetto del rumore. La stima può essere controllata dalla variabile delta, presente nel codice precedente, che ha anche l’effetto di ridurre la reattività del filtro alle variazioni del “vero” rapporto di copertura non osservato tra i due ETF.
Quando dobbiamo sviluppare una strategia di trading, è necessario ottimizzare questo parametro delta su panieri di coppie di ETF, utilizzando ancora una volta la convalida incrociata.
Prossimi passi
Ora che siamo stati in grado di costruire un rapporto di copertura dinamico tra i due ETF, abbiamo bisogno di un modo per realizzare effettivamente una strategia di trading basata su queste informazioni. A tale scopo si può utilizzare DataTrader per eseguire un backtest su varie coppie al fine di vedere come cambiano le prestazioni al variare dei parametri e degli intervalli temporali.
Nota bibliografica
L’utilizzo del filtro di Kalman per la “regressione lineare online” è stato eseguito da molti quant trader. Ernie Chan utilizza la tecnica nel suo libro [1] per stimare i coefficienti di regressione lineare dinamica tra i due ETF: EWA ed EWC.
Aidan O’Mahony ha utilizzato matplotlib e pykalman anche per stimare i coefficienti di regressione nel suo post [2].
Jonathan Kinlay discute l’applicazione del filtro di Kalman ai dati finanziari simulati [3] e suggerisce che potrebbe essere consigliabile utilizzare il KF per sopprimere i segnali di trading generati in periodi di forte rumore, o aumentare le allocazioni alle coppie in cui il rumore è basso.
Una discussione introduttiva sul filtro Kalman, utilizzando il linguaggio di programmazione R, può essere trovata in Cowpertwait e Metcalfe [4].
Riferimenti
- [1] Chan, E.P. (2013). Algorithmic Trading: Winning Strategies and Their Rationale.
- [2] O’Mahony, A. (2014). Online Linear Regression using a Kalman Filter
- [3] Kinlay, J. (2015). Statistical Arbitrage Using the Kalman Filter
- [4] Cowpertwait, P.S.P. and Metcalfe, A.V. (2009). Introductory Time Series with R.
- [5] Pole, A., West, M., and Harrison, J. (1994). Applied Bayesian Forecasting.
Codice completo
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import yfinance as yf
from pykalman import KalmanFilter
def draw_date_coloured_scatterplot(etfs, prices):
"""
Creare un grafico scatterplot dei prezzi di due ETF, che è
colorato dalle date dei prezzi per indicare il cambiamento
della relazione tra le due serie di prezzi
"""
# Creare a una mappa di colore da giallo a rosso dove il giallo
# indica le date più vecchie e il rosso indica le date recenti
# early dates and red indicates later dates
plen = len(prices)
colour_map = plt.cm.get_cmap('YlOrRd')
colours = np.linspace(0.1, 1, plen)
# Creare l'oggetto scatterplot
scatterplot = plt.scatter(
prices[etfs[0]], prices[etfs[1]],
s=30, c=colours, cmap=colour_map,
edgecolor='k', alpha=0.8
)
# Aggiungere una barra di colori per la colorazione dei dati ed
# impostare le etichette dell'asse corrispondente
colourbar = plt.colorbar(scatterplot)
colourbar.ax.set_yticklabels(
[str(p.date()) for p in prices[::plen // 9].index]
)
plt.xlabel(prices.columns[0])
plt.ylabel(prices.columns[1])
plt.show()
def calc_slope_intercept_kalman(etfs, prices):
"""
Utilizzo del filtro Kalman dal pacchetto pyKalman
per calcolare la pendenza e l'intercetta della
regressione lineare dei prezzi degli ETF.
"""
delta = 1e-5
trans_cov = delta / (1 - delta) * np.eye(2)
obs_mat = np.vstack(
[prices[etfs[0]], np.ones(prices[etfs[0]].shape)]
).T[:, np.newaxis]
kf = KalmanFilter(
n_dim_obs=1,
n_dim_state=2,
initial_state_mean=np.zeros(2),
initial_state_covariance=np.ones((2, 2)),
transition_matrices=np.eye(2),
observation_matrices=obs_mat,
observation_covariance=1.0,
transition_covariance=trans_cov
)
state_means, state_covs = kf.filter(prices[etfs[1]].values)
return state_means, state_covs
def draw_slope_intercept_changes(prices, state_means):
"""
Tracciare la variazione di pendenza e intercetta
dai valori calcolati dal Filtro di Kalman.
"""
pd.DataFrame(
dict(
slope=state_means[:, 0],
intercept=state_means[:, 1]
), index=prices.index
).plot(subplots=True)
plt.show()
if __name__ == "__main__":
# Scegliere i simboli ETF symbols e il periodo temporale
# dei prezzi storici
etfs = ['TLT', 'IEI']
start_date = "2012-10-01"
end_date = "2017-10-01"
# Download dei prezzi di chiusura da Yahoo finance
prices = yf.download(etfs, start=start_date, end=end_date)['Adj Close']
draw_date_coloured_scatterplot(etfs, prices)
state_means, state_covs = calc_slope_intercept_kalman(etfs, prices)
draw_slope_intercept_changes(prices, state_means)