In questo articolo descriviamo la nostra prima strategia di trading intraday. Si basa su una classica idea di trading, quella del ” trading pairs”. In questo caso si utilizza due Exchange Traded Funds (ETF), SPY e IWM, negoziati sul New York Stock Exchange (NYSE) e confrontarli rispettivamente con gli indici azionari statunitensi, l’S&P500 e il Russell 2000.
La strategia si base sul creare uno “spread” tra la coppia di ETF, andando long su un ETF e short sull’altro. Il rapporto tra long e short può essere definito in molti modi, ad esempio utilizzando tecniche di cointegrazione statistica sulle serie temporali. In questo esempio si calcola il “hedge ratio” (rapporto di copertura) tra SPY e IWM tramite una regressione lineare a rotazione. Questo permette
di creare un “spread” tra SPY e IWM che viene normalizzato in uno z-score. I segnali di trading sono generati quando lo z-score supera una determinata soglia, nella convinzione che lo spread tornerà verso la media.
La logica della strategia prevede che SPY e IWM sono caratterizzate approssimativamente dallo stesso comportamento o andamento, cioè rispettivamente quello di un gruppo di società statunitensi a grande capitalizzazione e quello delle società “small cap”. L’idea base considera che lo spread dei prezzi ha un comportamento mean-reverting, dal momento che eventi “locali” (nel tempo) possono influenzare separatamente gli indici S&P500 o Russell 2000 (come differenze di capitalizzazione, date di ribilanciamento o operazioni di blocco) ma nel lungo termine le serie di prezzi tendono ad essere cointegrate.
La Strategia
La strategia prevede i seguenti passaggi:
- Dati: ricavare le barre da 1 minuto di SPY e IWM dall’aprile 2007 a febbraio 2014.
- Elaborazione: allineare i dati ottenuti e eliminare reciprocamente le barre mancanti.
- Spread – calcolare il rapporto di copertura tra i due ETF prendendo una regressione lineare a rotazione. Questo è definito come il coefficiente di regressione \(β\), si ricalcola i coefficienti di regressione utilizzando una finestra che si sposta in avanti di 1 barra alla volta. Quindi calcolare il hedge ratio \(β_i\) per la barra \(b_i\) attraverso tutti i punti da \(b_i-1-k\) a \(b_i-1 per le \(\)k\) barre precedenti.
- Z-score – calcolare Il punteggio standard dello spread sottraendo la media (sample) dello spread e dividendo per la deviazione standard (sample) dello spread. In questo modo i parametri di soglia diventano più semplici da interpretare poiché il z-score è una quantità senza dimensione. E’ stato deliberatamente introdotto un bias di lookhead nei calcoli per mostrare quanto sia sensibile questo paramentro. Prova e trovarlo!
- Trade – generare i segnali long quando lo z-score negativo scende al di sotto di una predeterminata soglia (o post-ottimizzata), mentre i segnali short sono l’opposto di quelli long. Generare i segnali di uscita quando lo z-score assoluto scende al di sotto di una soglia aggiuntiva. Per questa strategia si è (in qualche modo arbitrariamente) scelta una soglia di ingresso assoluta di | z | = 2 e una soglia di uscita pari a | z | = 1. Supponendo che lo spread abbia un comportamento mean-reverting, si spera di catturare tale natura e fornire prestazioni positive.
Forse il modo migliore per comprendere a fondo la strategia è implementarla concretamente. La seguente sezione descrive un codice Python completo (singolo file) per l’implementazione di questa strategia di mean-reverting.
Implementazione in Python
Come per tutti i tutorial con Python e Pandas, è necessario aver impostato un ambiente di backtesting con Python, come descritto in questo tutorial. Una volta impostato, il primo passo è importare le necessarie librerie Python. Per questo backtest sono richiesti matplotlib e pandas.
In particolare si utilizzano le seguenti librerie:
- Python
- NumPy
- Pandas
- Matplotlib
- Statsmodels
di seguito il codice che importa tali librerie:
# mr_spy_iwm.py
import matplotlib.pyplot as plt
import numpy as np
import os, os.path
import pandas as pd
import seaborn as sns
import statsmodels.api as sm
from statsmodels.regression.rolling import RollingOLS
sns.set_style("darkgrid")
create_pairs_dataframe importa due file CSV contenenti le barre intraday di due simboli. Nel nostro caso questo sarà SPY e IWM. Si crea quindi il nuovo dataframe pairs, che usa gli indici di entrambi i file originali, questo garantisce di avere dati congruenti nel caso si abbiamo timestamp diversi tra le due serie a causa di errori e trade mancati. Questo è uno dei principali vantaggi di utilizzare una libreria di analisi dei dati come Pandas. Il codice “boilerplate” viene gestito per noi in modo molto efficiente.
# mr_spy_iwm.py
def create_pairs_dataframe(datadir, symbols):
"""
Crea un DataFrame pandas che contiene i prezzi di chiusura di una
coppia di simboli a partire da file CSV che contiene un datatime e
i dati OHLCV.
Parameters
----------
datadir : `str`
Directory dove sono archiviati file CSV che contengono i dati OHLCV.
symbols : `tup`
Tuple contenente i simboli ticker come `str`.
Returns
-------
pairs : `pd.DataFrame`
Un DataFrame contanente i prezzi di chiusura per SPY e IWM. L'indice è un
oggetto Datetime.
"""
# Apre i file CSV individualmente e legge il contenuto in un DataFrames pandas
# usando la prima colonna come un indice e col_names per gli headers
print("Importing CSV data...")
col_names = ['datetime', 'open', 'high', 'low', 'close', 'volume', 'na']
sym1 = pd.read_csv(
os.path.join(datadir, '%s.csv' % symbols[0]),
header=0,
index_col=0,
names=col_names
)
sym2 = pd.read_csv(
os.path.join(datadir, '%s.csv' % symbols[1]),
header=0,
index_col=0,
names=col_names
)
# Crea un DataFrame pandas con i prezzi di chiusura per ogni simbolo
# correttamente allineate e elimenanto gli elementi mancanti
print("Constructing dual matrix for %s and %s..." % symbols)
pairs = pd.DataFrame(index=sym1.index)
pairs['%s_close' % symbols[0].lower()] = sym1['close']
pairs['%s_close' % symbols[1].lower()] = sym2['close']
pairs.index = pd.to_datetime(pairs.index)
pairs = pairs.dropna()
return pairs
Il prossimo passo è eseguire la regressione lineare “rolling” tra SPY e IWM. In questo caso IWM è il predittore (‘x’) e SPY è la risposta (‘y’). Si prevede una finestra di ricerca predefinita pari a 100 barre. Come descritto in precedenza, questo è un parametro della strategia. Affinché la strategia sia considerata robusta, si desidera trovare una curva di equity (o altra misura di prestazione) che corrisponda a una funzione convessa del periodo di ricerca. Quindi in una fase successiva del codice effettueremo un’analisi di sensibilità variando il periodo di ricerca all’interno di un intervallo.
Dopo aver calcolato il coefficiente di rolling beta nel modello di regressione lineare per SPY-IWM, lo aggiungiamo al dataFrame pairs eliminando i record vuoti. Questo costituisce il primo set di barre di dimensione pari alla finestra di lookback. Si calcola quindi lo spread tra i due ETF come una unità di SPY \(-\beta_i\) unità di IWM. Chiaramente questo non è uno scenario realistico poiché si considerano piccole quantità di IWM, che non è possibile in una implementazione reale.
Infine si crea lo z-score dello spred, calcolato sottraendo ogni unità con la media dello spread e normalizzando il risultato con la deviazione standard dello stesso spread. Da notare che con questo approccio si genera un bias di lookahead. E’ stato deliberatamente inserito nel codice al fine di enfatizzare la facilità con cui si può commettere un tale errore durante la fase di ricerca. La media e la deviazione standard sono calcolate a partire da tutta la serie temporale dello spread. Anche se questo permette di modellare la reale accuratezza storica, tale informazione non sarebbe disponibile nel live trading dato che utilizza implicitamente dati futuri. Quindi dovremmo usare una media e una deviazione standard mobili per calcolare lo z-score.
# mr_spy_iwm.py
def calculate_spread_zscore(pairs, symbols, lookback=100):
"""
Crea un hedge ratio tra i due simboli calcolando una regressione
lineare mobile con uno specifico periodo di lookback. Questa è
usata per creare uno z-score dello 'spread' tra i due simboli
basato da una combinazione lineare dei due.
Parameters
----------
pairs : `pd.DataFrame`
Un DataFrame contanente i prezzi di chiusura per SPY e IWM. L'indice è un
oggetto Datetime.
symbols : `tup`
Tuple contenente i simboli ticker come `str`.
lookback : `int`, optional (default: 100)
Periodo di Lookback per la regressione lineare mobile.
Returns
-------
pairs : 'pd.DataFrame'
Aggiornamento del DataFrame con lo spred e lo z score tra i
due simboli basati sulla regressione lineare mobile.
"""
# Uso del metodo Rolling Ordinary Least Squares di statsmodels per allenare
# una regressione lineare mobile tra le due serie temporali dei prezzi di chiusura
print("Fitting the rolling Linear Regression...")
model = RollingOLS(
endog=pairs['%s_close' % symbols[0].lower()],
exog=sm.add_constant(pairs['%s_close' % symbols[1].lower()]),
window=lookback
)
rres = model.fit()
params = rres.params.copy()
# Costruzione del hedge ratio ed eliminazione del primo elemento della
# finestra di lookbackand vuoto/NaN
pairs['hedge_ratio'] = params['iwm_close']
pairs.dropna(inplace=True)
# Crea uno spread e quindi uno z-score dello spread
print("Creating the spread/zscore columns...")
pairs['spread'] = (pairs['spy_close'] - pairs['hedge_ratio'] * pairs['iwm_close'])
pairs['zscore'] = (pairs['spread'] - np.mean(pairs['spread'])) / np.std(pairs['spread']
)
return pairs
Nel metodo create_long_short_market_signals si generano i segnali di trading. In particolare, sono generati segnali “long” quando lo z-score diventa inferiore ad una certa soglia negativa, mentre sono generati segnali “short” quando lo z-score diventa maggiore a una soglia positiva. Il segnale di uscita viene generato quando il valore assoluto dello z-score è uguale o inferiore ad un’altra specifica soglia (di valore inferiore).
Inoltre questa strategia prevede la verifica delle posizioni già aperte, cioè per ogni barra è necessario conoscere se la strategia è “in” o “out” dal mercato. Si usano le due variabili long_market e short_market per tenere traccia delle posizioni long e short aperte sul mercato. Sfortunatamente questo è molto più semplice da codificare in modo iterativo rispetto a un approccio vettorializzato ma l’elaborazione di calcolo è più lenta. Nonostante ogni file CSV contenga circa 700.000 punti dati corrispondenti a barre di 1 minuto, l’elaborazione è relativamente veloce anche su una normale macchina desktop!
Per eseguire un’iterazione su un dataFrame di Pandas (che in effetti NON è un’operazione comune) è necessario utilizzare il metodo iterrows, che fornisce un generatore su cui eseguire iterazioni:
# mr_spy_iwm.py
def create_long_short_market_signals(pairs, symbols, z_entry_threshold=2.0, z_exit_threshold=1.0):
"""
Crea i segnali di entrata/uscita in base al superamento di z_entry_threshold
per entrare in una posizione e al di sotto di z_exit_threshold per
uscire da una posizione.
Parameters
----------
pairs : `pd.DataFrame`
DataFrame aggiornato contenente il prezzo di chiusura, lo spread
e il punteggio z tra i due simboli.
symbols : `tup`
Tupla contenente simboli ticker come `str`.
z_entry_threshold : `float`, optional (default:2.0)
Soglia di punteggio Z per l'ingresso nel mercato.
z_exit_threshold : `float`, optional (default:1.0)
Soglia di punteggio Z per l'uscita dal mercato.
Returns
-------
pairs : `pd.DataFrame`
DataFrame aggiornato contenente segnali long, short e di uscita
"""
# Calcola quando essere long, short e quando uscire
pairs['longs'] = (pairs['zscore'] <= -z_entry_threshold)*1.0
pairs['shorts'] = (pairs['zscore'] >= z_entry_threshold)*1.0
pairs['exits'] = (np.abs(pairs['zscore']) <= z_exit_threshold)*1.0
# Questi segnali sono necessari perché dobbiamo propagare
# una posizione in avanti, ovvero dobbiamo rimanere long se
# la soglia zscore è inferiore a z_entry_threshold di ancora
# maggiore di z_exit_threshold, e viceversa per short.
pairs['long_market'] = 0.0
pairs['short_market'] = 0.0
# Queste variabili tracciano se essere long o short
# durante l'iterazione tra le barre
long_market = 0
short_market = 0
# Poiché utilizza iterrows per eseguire il loop su un dataframe,
# sarà significativamente meno efficiente di un'operazione vettorializzata,
# cioè più lenta!
print("Calculating when to be in the market (long and short)...")
for i, b in enumerate(pairs.iterrows()):
# Calcola i long
if b[1]['longs'] == 1.0:
long_market = 1
# Calcola gli short
if b[1]['shorts'] == 1.0:
short_market = 1
# Calcola le uscite
if b[1]['exits'] == 1.0:
long_market = 0
short_market = 0
# Assegna direttamente un 1 o 0 alle colonne long_market/short_market,
# in modo tale che la strategia sappia quando effettivamente entrare!
pairs.iloc[i]['long_market'] = long_market
pairs.iloc[i]['short_market'] = short_market
return pairs
A questo punto le pairs sono aggiornate per gestire i segnali long / short in essere, in modo da determinare se ci sono posizioni aperte a mercato. Quindi si crea un portfolio per tenere traccia del valore di mercato delle posizioni aperte. Il primo passo è creare una colonna delle posizioni che combini i segnali long e short. Questa colonna contiene un elenco di elementi da (1, 0, -1), con 1 che rappresenta una posizione long / market, 0 che non rappresenta alcuna posizione (o che dovrebbe essere chiusa) e -1 che rappresenta una posizione short / market. Le colonne sym1 e sym2 rappresentano i valori di mercato delle posizioni SPY e IWM per ogni barra.
Dopo aver creato i valori di mercato relativi agli strumenti ETF, questi sono sommati per ricavare il valore totale di esposizione sul mercato, per ogni barra. Questo viene quindi trasformato in un flusso di rendimenti mediante il metodo pct_change dell’oggetto Series. Le successive righe di codice permetto di cancellare le voci errate (elementi NaN e inf) e di calcolare l’intera curva di equity.
# mr_spy_iwm.py
def create_portfolio_returns(pairs, symbols):
"""
Crea un DataFrame pandas di portafoglio che tiene traccia del
capitale dell'account e alla fine genera una curva di equity.
Questo può essere utilizzato per generare drawdown e rapporti
rischio/rendimento.
Parameters
----------
pairs : `pd.DataFrame`
DataFrame aggiornato contenente il prezzo di chiusura, lo spread
e il punteggio z tra i due simboli e i segnali long, short e uscita.
symbols : `tup`
Tupla contenente simboli ticker come `str`.
Returns
-------
portfolio : 'pd.DataFrame'
Un DataFrame con l'indice datetime del DataFrame dei pairs, le posizioni,
il valore di mercato totale e rendimenti.
"""
# Variabili di convenzione per i simboli
sym1 = symbols[0].lower()
sym2 = symbols[1].lower()
# Crea l'oggetto portfolio con le informazioni sulle posizioni
# Notare la sottrazione per tenere traccia degli short!
print("Constructing a portfolio...")
portfolio = pd.DataFrame(index=pairs.index)
portfolio['positions'] = pairs['long_market'] - pairs['short_market']
portfolio[sym1] = -1.0 * pairs['%s_close' % sym1] * portfolio['positions']
portfolio[sym2] = pairs['%s_close' % sym2] * portfolio['positions']
portfolio['total'] = portfolio[sym1] + portfolio[sym2]
# Crea un flusso di rendimenti percentuali ed elimina
# tutte le celle NaN e -inf/+inf
print("Constructing the equity curve...")
portfolio['returns'] = portfolio['total'].pct_change()
portfolio['returns'].fillna(0.0, inplace=True)
portfolio['returns'].replace([np.inf, -np.inf], 0.0, inplace=True)
portfolio['returns'].replace(-1.0, 0.0, inplace=True)
# Calcola la curva di equity
portfolio['returns'] = (portfolio['returns'] + 1.0).cumprod()
return portfolio
La funzione __main__ collega tutto insieme. Il path dei file CSV è memorizzato nella viaribile datadir. Bisogna modificare questa variabile al fine da puntare alla propria specifica directory.
Per determinare la sensibilità della strategia rispetto al periodo di ricerca, è necessario calcolare una metrica di performarce in un range di intervalli. In questo caso si usa il rendimento percentuale totale del portfolio come misura di performance e l’intervallo di ricerca pari a [50, 200] con incrementi di 10. Inoltre si osservi che le funzioni descritte in precedenza sono racchiuse all’interno di un ciclo for che attraversa lo specifico intervallo, mentre le altre soglie sono mantenute costanti. L’ultimo passo è usare matplotlib per creare un grafico a linee dei lookbacks vs returns:
# mr_spy_iwm.py
if __name__ == "__main__":
datadir = '/your/path/to/data/' # Da modificare
symbols = ('SPY', 'IWM')
lookbacks = range(50, 210, 10)
returns = []
# Regola il periodo di ricerca da 50 a 200 con
# incrementi di 10 per produrre sensibilità
for lb in lookbacks:
print("Calculating lookback=%s..." % lb)
pairs = create_pairs_dataframe(datadir, symbols)
pairs = calculate_spread_zscore(pairs, symbols, lookback=lb)
pairs = create_long_short_market_signals(
pairs, symbols, z_entry_threshold=2.0, z_exit_threshold=1.0
)
portfolio = create_portfolio_returns(pairs, symbols)
returns.append(portfolio.iloc[-1]['returns'])
print("Plot the lookback-performance scatterchart...")
plt.plot(lookbacks, returns, '-o')
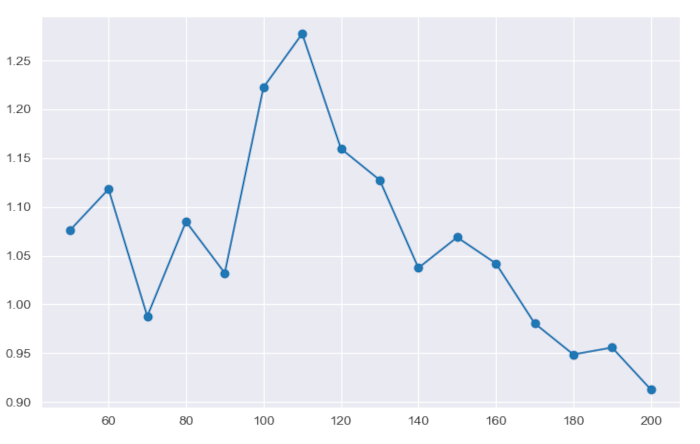
plt.show()
Ora è possibile visualizzare il grafico dei rendimenti risposto all’intervallo di ricerca (numero di barre). Da notare la presenza di un massimo “globale” attorno alle 110 barre. Sarebbe stato preoccupante un risultato dove l’intervallo di ricerca fosse stato indipendente dai rendimenti:
# mr_spy_iwm.py
# Questo è ancora nella funzione main
pairs = create_pairs_dataframe(datadir, symbols)
pairs = calculate_spread_zscore(pairs, symbols, lookback=100)
pairs = create_long_short_market_signals(
pairs, symbols, z_entry_threshold=2.0, z_exit_threshold=1.0
)
portfolio = create_portfolio_returns(pairs, symbols)
print("Plotting the performance charts...")
fig = plt.figure()
ax1 = fig.add_subplot(211, ylabel='%s growth (%%)' % symbols[0])
(pairs['%s_close' % symbols[0].lower()].pct_change()+1.0).cumprod().plot(ax=ax1, color='r', lw=2.)
ax2 = fig.add_subplot(212, ylabel='Portfolio value growth (%%)')
portfolio['returns'].plot(ax=ax2, lw=2.)
plt.show()
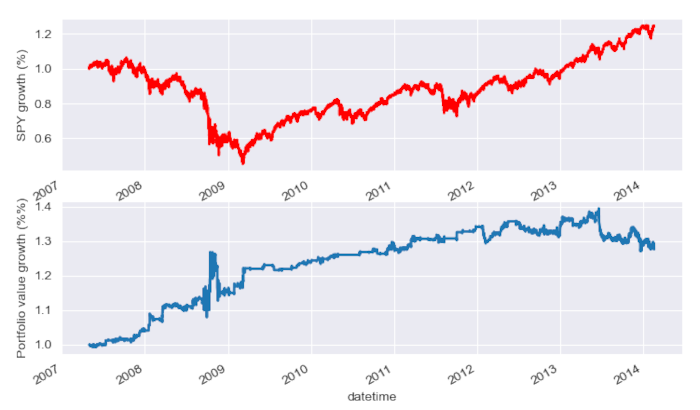
Da notare il significativo drawdown di SPY nel 2009, durante il periodo della crisi finanziaria. In questo periodo la strategia ha avuto un’elevata volatilità. Inoltre la performance è leggermente peggiorata nell’ultimo anno a causa della natura fortemente trending di SPY in questo periodo, che riflette l’indice S&P500.
Infine da notare che il bias di lookahead è ancora presente durante il calcolo dello z-score e non sono stati considerati i costi di transazione. Questa strategia funzionerebbe molto male una volta presi in considerazione questi fattori. Le commisioni, lo spread bid / ask e lo slippage non sono implementate e, inoltre, la strategia opera con unità frazionarie di ETF, che è una situazione molto irrealistica.
Per tenere conto di questi fattori e fornire una migliore curva di equity e parametri di performance più affidabili si deve utilizzare un ambiente di backtesting basato sugli eventi, descritto in questa serie di articoli.
Per il codice completo riportato in questo articolo utilizzando il modulo di backtesting vettoriale VectorBacktest si può consultare il seguente repository di github:
https://github.com/datatrading-info/VectorBacktest