In questo articolo descriviamo come implementare un asset allocation tramite modello di Black-Litterman in Python. Nel precedente articolo “Ottimizzare l’asset allocation di un portafoglio con Python” abbiamo introdotto il processo di calcolo dei pesi ottimali degli asset in un portafoglio secondo il classico approccio “media-varianza” di Markowitz.
Con questo metodo miriamo a massimizzare il nostro livello di rendimento per ogni dato livello di rischio, così facendo sviluppiamo il concetto di “frontiera efficiente” e solitamente cerchiamo di identificare il punto/portafoglio su quella frontiera che rappresenta il miglior compromesso tra rischio e rendimento (ovvero il portafoglio con lo Sharpe Ratio più elevato).
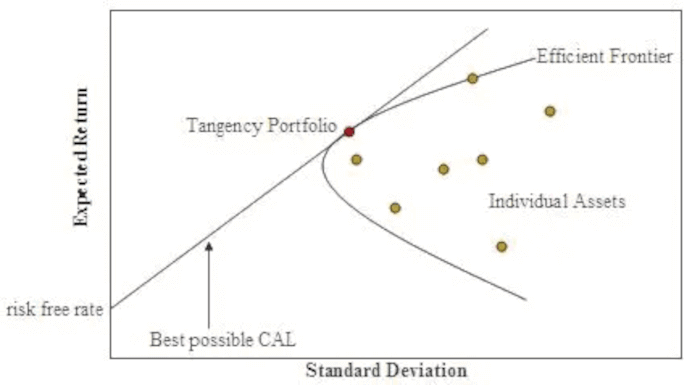
Nonostante il modello permette di identificare i nostri presunti “pesi ottimali degli asset”, ci sono diverse criticità, alcune gravi, che dobbiamo affrontare quando utilizziamo l’ottimizzazione della media-varianza.
- Il modello presuppone che i rendimenti degli asset hanno una distribuzione normale.
- Può generare portafogli non intuitivi e altamente concentrati.
- Gli input del modello includono il rendimento previsto/atteso e la volatilità di ogni singolo asset, ma ovviamente non potremo mai conoscere tali valori con certezza. La pratica comune è quella di calcolare i rendimenti storici e le deviazioni standard degli asset e usarli come proxy. In questo modo si presume che tutti gli asset continueranno a comportarsi come hanno fatto in passato. Non solo si presuppone che i rendimenti e la volatilità rimarranno gli stessi, ma si presuppone che le correlazioni tra tutti gli asset in questione rimarranno stabili nel tempo. Sappiamo che queste ipotesi semplicemente non sono realistiche.
- A peggiorare le cose, non solo utilizziamo input che fanno affidamento sulle nostre “migliori ipotesi” o previsioni, ma il modello risulta essere estremamente sensibile alle variazioni di questi valori di input (in particolare agli input di rendimento, meno agli input di volatilità). Se modifichiamo i valori di input, anche con importi relativamente piccoli, i pesi ottimali del portafoglio create dal modello possono oscillare e variare notevolmente. Idealmente, vorremo che il modello fosse il più “robusto” possibile e generasse pesi stabili o che cambiano lentamente di fronte alla variazione dei valori di input.
In questo articolo approfondiamo il modello Black-Litterman, che è un adattamento del classico modello media-varianza. Questo modello permette agli investitori di combinare le loro opinioni relative alle performance dei vari asset con l’equilibrio del mercato in un modo da ottenere portafogli intuitivi e diversificati.
Il modello Black-Litterman
Il modello Black-Litterman usa un approccio bayesiano per combinare le opinioni soggettive di un investitore riguardo ai rendimenti attesi di uno o più asset con il vettore di equilibrio di mercato dei rendimenti attesi (la distribuzione a priori) per formare una nuova stima mista dei rendimenti attesi. Il nuovo vettore di rendimenti (la distribuzione a posteriori) permette di creare portafogli intuitivi con pesi ragionevoli.
Questo modello combina il classico concetto di CAPM, l’ottimizzazione inversa, la stima mista, il “rapporto di copertura universale”/CAM globale e infine l’ottimizzazione media-varianza, che sappiamo essere la base del classico modello di Markowitz, descritto in precedenza.
Il problema della sensibilità agli input è superato nel modello Black-Litterman mediante l’uso dell’ottimizzazione inversa per annullare il vettore dei rendimenti richiesti dagli asset (valori) anziché essere un input “esogeno” come nel caso del modello media-varianza. Iniziamo con il concetto dei rendimenti di “equilibrio” come punto di partenza neutrale: l’insieme di “equilibrio” è l’insieme dei rendimenti richiesti affinché l’asset allocation di equilibrio sia uguale a quella che osserviamo nei mercati. In altre parole possiamo calcolare il valore di mercato di un determinato insieme di asset o classi di asset in modo abbastanza accurato, e quindi usare questi valori di mercato per estrarre il livello dei rendimenti che il mercato deve aspettarsi in futuro per quegli asset.
Iniziamo con i rendimenti di equilibrio perchè in questo modo otteniamo una “ragionevole” serie di valori per i rendimenti previsti, che si basano su solide basi economiche. Successivamente, più avanti nel processo, l’investitore ha la possibilità di incorporare nei valori di input eventuali opinioni o convinzioni soggettive che potrebbe avere, regolando di conseguenza i valori di input.
Vediamo come calcolare esattamente i rendimenti di equilibrio. Possono essere calcolati tramite un metodo di ottimizzazione inversa dove il vettore dei rendimenti di equilibrio impliciti in eccesso è estratto dalle informazioni note, usando la seguente formula:

Vale la pena notare che il parametro dell’avversione al rischio viene impostato secondo approcci diversi. Alcuni impostano il valore del parametro di avversione al rischio tra 2,15 e 2,65 (poiché questi valori sono stati le raccomandazioni risultanti da varie ricerche accademiche sull’argomento).
Altri fissano il valore uguale al “prezzo di mercato del rischio” (ovvero l’avversione al rischio dell’”Investitore rappresentativo”) che viene calcolato come \(\lambda = \mu_{m} / \sigma_{m}^2\) (cioè il rendimento medio del portafoglio del mercato globale diviso per la sua varianza). Usiamo questo metodo per impostare il valore del parametro di avversione al rischio a breve.
Riorganizzando la formula precedente e sostituendo con \(\mu * \Pi\) (con \(\mu\) che rappresenta qualsiasi vettore di rendimento in eccesso e \(\Pi\) che rappresenta il vettore dei rendimenti di equilibrio in eccesso impliciti) otteniamo la seguente formula:
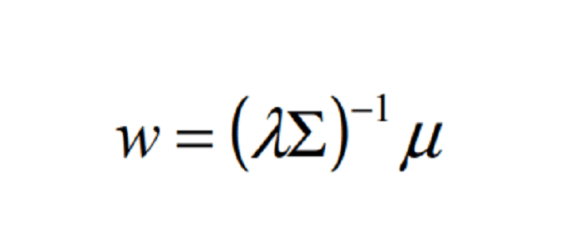
che è la soluzione del problema di massimizzazione non vincolata:
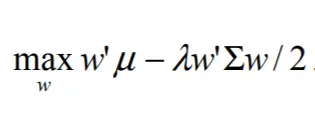
cioè per avere \(w\) uguale a \(w_{mkt}\), dobbiamo avere \(\mu\) uguale a \(\Pi\).
I rendimenti storici
Iniziamo caricando i dati sui rendimenti storici per l’universo delle classi di asseti che vogliamo includere nel portafoglio globale da file CSV, insieme ai dati relativi ai pesi basati sulla capitalizzazione di mercato di ciascun asset. I file di input che vogliamo usare possono essere scaricati dai seguenti link:
import numpy as np
import pandas as pd
from numpy.linalg import inv
asset_returns_orig = pd.read_csv('rendimenti_asset.csv', index_col='Year', parse_dates=True)
asset_weights = pd.read_csv('pesi_asset.csv', index_col='asset_class')
cols = ['Global Bonds (Unhedged)', 'Total US Bond Market', 'US Large Cap Growth',
'US Large Cap Value', 'US Small Cap Growth', 'US Small Cap Value', 'Emerging Markets',
'Intl Developed ex-US Market', 'Short Term Treasury']
asset_returns = asset_returns_orig[cols].dropna()
treasury_rate = asset_returns['Short Term Treasury']
asset_returns = asset_returns[cols[:-1]].astype(float).dropna()
asset_weights = asset_weights.loc[cols[:-1]]
Possiamo stampare i rendimenti medi annuali e i pesi di ciascuna classe di asset come mostrato di seguito:
print(asset_returns.mean())
Global Bonds (Unhedged) 0.059615
Total US Bond Market 0.054231
US Large Cap Growth 0.131538
US Large Cap Value 0.102308
US Small Cap Growth 0.119615
US Small Cap Value 0.114615
Emerging Markets 0.100000
Intl Developed ex-US Market 0.063462
dtype: float64
print(asset_weights)
asset_class weight
Global Bonds (Unhedged) 0.224
Total US Bond Market 0.077
US Large Cap Growth 0.163
US Large Cap Value 0.162
US Small Cap Growth 0.022
US Small Cap Value 0.022
Emerging Markets 0.030
Intl Developed ex-US Market 0.299
Successivamente sottraiamo il tasso degli interessi a breve termine dai rendimenti della classe di asset per ottenere i relativi “rendimenti in eccesso” necessari per generare la matrice di varianza-covarianza dei rendimenti in eccesso. Calcoliamo quindi il rendimento medio e la varianza del portafoglio del mercato globale:
excess_asset_returns = asset_returns.subtract(treasury_rate, axis=0)
cov = excess_asset_returns.cov()
global_return = excess_asset_returns.mean().multiply(asset_weights['weight'].values).sum()
market_var = np.matmul(asset_weights.values.reshape(len(asset_weights)).T,
np.matmul(cov.values, asset_weights.values.reshape(len(asset_weights))))
print(f'The global market mean return is {global_return:.4f} and the variance is {market_var:.6}')
risk_aversion = global_return / market_var
print(f'The risk aversion parameter is {risk_aversion:.2f}')
The global market mean return is 0.0446 and the variance is 0.0202548
The risk aversion parameter is 2.20
Implementiamo la funzione per decodificare i pesi di un portafoglio in modo da ottenere il vettore dei rendimenti di equilibrio impliciti.
def implied_rets(risk_aversion, sigma, w):
implied_rets = risk_aversion * sigma.dot(w).squeeze()
return implied_rets
implied_equilibrium_returns = implied_rets(risk_aversion, cov, asset_weights)
print(implied_equilibrium_returns)
Global Bonds (Unhedged) 0.012871
Total US Bond Market 0.002439
US Large Cap Growth 0.060436
US Large Cap Value 0.051548
US Small Cap Growth 0.056798
US Small Cap Value 0.043902
Emerging Markets 0.076184
Intl Developed ex-US Market 0.063076
Name: weight, dtype: float64
In questa fase è importante familiarizzare con la “Formula di Black-Litterman”. In questo articolo, usiamo K per rappresentare il numero di viste e N per esprimere il numero di asset nella formula. La formula per il nuovo vettore dei rendimenti combinati è:

Includere le previsioni soggettive
Molto spesso, i gestori di investimenti hanno opinioni specifiche riguardo al rendimento atteso di alcuni asset in un portafoglio, che differiscono dal rendimento di equilibrio implicito. Il modello Black-Litterman consente di esprimere tali opinioni in termini assoluti o relativi.
Impostiamo 3 viste che potremmo avere riguardo ad alcuni degli asset nel nostro portafoglio:
- Vista 1: I “Mercati emergenti” avranno un extra rendimento assoluto del 9,25% (rispetto al valore di equilibrio del 7,62%)
- Vista 2: La crescita delle large cap Growth e delle small cap Growth statunitensi supererà il valore delle large cap Value e delle small cap Value statunitensi del 0,5% (rispetto al valore di equilibrio basato sull’1%-1,2%)
- Vista 3: Il “Mercato internazionale sviluppato ex-USA” avrà un extra rendimento assoluto del 5,5% (rispetto al valore di equilibrio del 6,31%).
Le viste 1 e 3 sono esempi di visione assoluta, mentre la visione 2 è una visione relativa. Le viste di tipo relativo tendono a rappresentare più da vicino il modo in cui la maggior parte dei gestori di denaro/investimenti vede il mondo e come si sente riguardo ai diversi asset.
Nel nostro esempio, il numero di viste (K) è 3; quindi, il vettore delle viste (Q) è un vettore 3 x 1. L’incertezza delle opinioni si traduce in un vettore dei termini di errore casuale, sconosciuto, indipendente e normalmente distribuito (\(\epsilon\)) con media pari a 0 e matrice di covarianza \(\Omega\). Pertanto, una vista ha la forma \(\Omega+\epsilon\).
Il vettore dei termini di errore (\(\epsilon\)) non entra direttamente nella formula di Black-Litterman. Tuttavia, la varianza di ciascun termine di errore (\(\omega\)), che rappresenta la differenza assoluta rispetto al termine di errore atteso (\(\epsilon\)) pari a 0, è presente nella formula. Le varianze dei termini di errore (\(\omega\)) formano \(\Omega\), che è una matrice delle covarianze con 0 in tutte le posizioni fuori diagonale. Gli elementi fuori dalla diagonale sono 0 perché il modello presuppone che le viste siano indipendenti l’una dall’altra. Le varianze dei termini di errore rappresentano l’incertezza delle opinioni. Maggiore è la varianza del termine di errore, maggiore è l’incertezza della vista.
Il nostro vettore Q è il seguente:
Q = np.array([0.0925, 0.005, 0.055])
Ora impostiamo la matrice P dove inseriamo le nostre opinioni. Dato che abbiamo 3 viste e 8 asset, creiamo una matrice 3 per 8 come la seguente:
P = [[0, 0, 0, 0, 0, 0, 1, 0],
[0, 0, .5, -.5, .5, -.5, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 1]]
La prima riga della matrice P rappresenta la vista 1, dove “Mercati emergenti” è l’asset interessato. La settima posizione die questa riga rappresenta la settima classe di asset nel nostro esempio (ovvero la settima colonna nei nostri DataFrames originali (“rendimenti_asset” e “pesi_asset”)).
La vista 2 e la vista 3 sono rappresentate rispettivamente dalla riga 2 e dalla riga 3.
Pesi in base alla capitalizzazione di mercato
L’approccio di cui sopra può essere considerato un approccio di “equa ponderazione” che a volte può causare cambiamenti relativamente ampi nei pesi proposti per le classi di asset più piccole. Alcuni metodi scelgono di ponderare i valori nella Matrice P in base alle loro capitalizzazioni di mercato in modo da evitare grandi oscillazioni nelle ponderazioni. In questo esempio vediamo come applicare questo metodo.
Dai pesi delle classi di asset mostrati nella nostra tabella, possiamo vedere che gli asset a grande capitalizzazione sono sufficientemente vicini a 8 volte la dimensione degli asset a piccola capitalizzazione. Nella nostra matrice P riflettiamo questo scenario come mostrato di seguito:
P = np.asarray([[0, 0, 0, 0, 0, 0, 1, 0],
[0, 0, .85, -.85, .15, -.15, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 1]])
view1_var = np.matmul(P[0].reshape(len(P[0])),np.matmul(cov.values, P[0].reshape(len(P[0])).T))
view2_var = np.matmul(P[1].reshape(len(P[1])),np.matmul(cov.values, P[1].reshape(len(P[1])).T))
view3_var = np.matmul(P[2].reshape(len(P[2])),np.matmul(cov.values, P[2].reshape(len(P[2])).T))
print(f'The Variance of View 1 Portfolio is {view1_var}, and the standard deviation is {np.sqrt(view1_var):.3f}\n',\
f'The Variance of View 2 Portfolio is {view2_var}, and the standard deviation is {np.sqrt(view2_var):.3f}\n',\
f'The Variance of View 3 Portfolio is {view3_var}, and the standard deviation is {np.sqrt(view3_var):.3f}')
The Variance of View 1 Portfolio is 0.09655215384615386, and the standard deviation is 0.311
The Variance of View 2 Portfolio is 0.014389680384615406, and the standard deviation is 0.120
The Variance of View 3 Portfolio is 0.04505784615384616, and the standard deviation is 0.212
Queste informazioni sono usate per rivisitare le varianze dei termini di errore (\(\omega\)) che formano gli elementi diagonali di \(\Omega\).
Ci sono diversi fattori in gioco che influenzano i risultati del modello Black-Litterman, che è concettualmente una media complessa e ponderata di:
- il vettore dei rendimento di equilibrio implicito (\(\Pi\))
- il vettore delle viste (\(Q\)) dove i pesi relativi sono funzione di:
- lo scalare (\(\tau\))
- l’incertezza delle opinioni (\(\Omega\))
Lo scalare (\(\tau\)) e l’incertezza delle opinioni (\(\Omega\)) sono i parametri del modello più difficili da specificare; maggiore è il livello di certezza o fiducia che il gestore esprime nelle opinioni, più vicino sarà il nuovo vettore dei rendimenti delle opinioni. Viceversa, minore è la fiducia del manager riguardo alla sua visione, il nuovo vettore dei rendimenti sarà più vicino al vettore originale dei rendimenti di equilibrio impliciti (\(\Pi\)).
Lo scalare tende ad essere più o meno inversamente proporzionale al peso che il modello attribuisce al vettore dei rendimenti di equilibrio impliciti (\(\Pi\)).
Lo scalare tende ad essere impostato secondo una serie di metodi diversi, a seconda dell’approccio che si vuole seguire:
- Impostare il valore dello scalare tra 0,01 e 0,05, quindi calibrare il modello in base a un livello target di tracking error.
- Impostare il valore dello scalare su 1.
- Impostare il valore dello scalare su 1 diviso per il numero di osservazioni.
Per gli asset oggetto di una vista, l’entità del loro allontanamento dal peso della capitalizzazione di mercato è controllata dal rapporto tra lo scalare (\(\tau\)) e la varianza del termine di errore (\(\omega\)) della vista in questione.
Calibrare il modello
Il modo più semplice per calibrare il modello di Black-Litterman è fare un’ipotesi sul valore dello scalare (\(\tau\)) che impostiamo pari a 0,025 e quindi impostiamo il rapporto \(\omega/\tau\) pari alla varianza del portafoglio della vista \(p_{k}\Sigma p_{k}{‘}\).
Usiamo il nostro valore di \(\tau\) e le varianze della vista individuale calcolate sopra, la nostra matrice di covarianza del termine di errore (\(\Omega\)) appare come segue (creiamo una funzione per generare la nostra matrice):
def error_cov_matrix(sigma, tau, P):
matrix = np.diag(np.diag(P.dot(tau * cov).dot(P.T)))
return matrix
tau = 0.025
omega = error_cov_matrix(cov, tau, P)
Ora calcoliamo il nostro nuovo vettore dei rendimento “basato sulla vista”:
sigma_scaled = cov * tau
BL_return_vector = implied_equilibrium_returns + sigma_scaled.dot(P.T).dot(inv(P.dot(sigma_scaled).dot(P.T) + omega).dot(Q - P.dot(implied_equilibrium_returns)))
Otteniamo il seguente risultato
print(BL_return_vector)
Global Bonds (Unhedged) 0.013157
Total US Bond Market 0.002431
US Large Cap Growth 0.057505
US Large Cap Value 0.050891
US Small Cap Growth 0.056636
US Small Cap Value 0.044942
Emerging Markets 0.079098
Intl Developed ex-US Market 0.062403
dtype: float64
Anche se le opinioni espresse riguardavano direttamente solo 6 delle 8 classi di asset, i rendimenti individuali di tutti gli asset sono cambiati rispetto ai relativi rendimenti di equilibrio impliciti. Confrontiamo il nuovo vettore dei rendimenti con il vettore dei rendimenti impliciti originale.
returns_table = pd.concat([implied_equilibrium_returns, BL_return_vector], axis=1) * 100
returns_table.columns = ['Implied Returns', 'BL Return Vector']
returns_table['Difference'] = returns_table['BL Return Vector'] - returns_table['Implied Returns']
returns_table.style.format('{:,.2f}%')
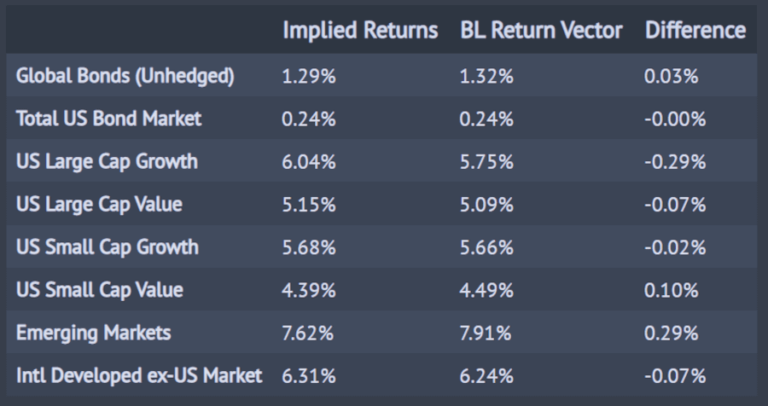
Vediamo che il rendimento della classe di asset “Mercati emergenti” è aumentato dello 0,29%, mentre il rendimento della classe di asset“Mercati internazionali sviluppati ex-USA” è diminuito dello 0,07%.
Le variazioni relative tra le classi di asset “US Large Cap Growth” e “US Large Cap Value”, e tra le classi di attività “US Small Cap Growth” e “US Small Cap Value” sono entrambe a favore degli asset “Value”. Ovvero le Large Cap Growth sono scese dello 0,29% mentre le Large Cap Value sono scesi solo dello 0,07%, e le Small Cap Growth sono scesi dello 0,02% mentre le Small Cap Value sono in realtà aumentate dello 0,1%.
Questi cambiamenti sono sensati dato che le nostre opinioni incorporavano un aumento assoluto del rendimento dei “Mercati emergenti”, una diminuzione assoluta del rendimento della classe “Mercato internazionale sviluppato ex-USA” e un aumento relativo della performance delle 2 classi US Value rispetto alle classi Growth USA. L’equilibrio riportava una differenza di circa l’1,2% a favore delle classi Growth, mentre secondo la nostra opinione era solo dello 0,5% a loro favore.
I risultati del modello
Ora possiamo calcolare il nuovo vettore dei pesi basato su Black Litterman come segue:
inverse_cov = pd.DataFrame(inv(cov.values), index=cov.columns, columns=cov.index)
BL_weights_vector = inverse_cov.dot(BL_return_vector)
BL_weights_vector = BL_weights_vector/sum(BL_weights_vector)
Confrontiamo il nuovo vettore dei pesi con i pesi originali della capitalizzazione di mercato riportati di seguito e con i pesi ottimizzati media-varianza (assumendo di utilizzare il rendimento annuale medio storico come input del vettore dei rendimenti):
# Calcola i pesi ottimizzati media-varianza
MV_weights_vector = inverse_cov.dot(excess_asset_returns.mean())
MV_weights_vector = MV_weights_vector/sum(MV_weights_vector)
weights_table = pd.concat([BL_weights_vector, asset_weights, MV_weights_vector], axis=1) * 100
weights_table.columns = ['BL Weights', 'Market Cap Weights', 'Mean-Var Weights']
weights_table['BL/Mkt Cap Diff'] = weights_table['BL Weights'] - weights_table['Market Cap Weights']
weights_table.style.format('{:,.2f}%')
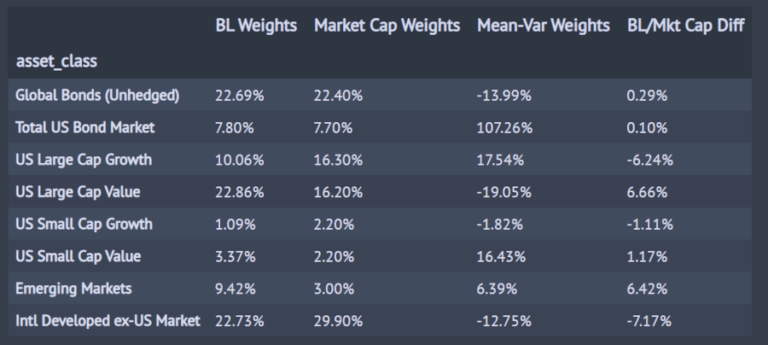
Osserviamo che:
- I pesi sono diminuiti per le classi “US Large Cap Growth” (-6,24%) e “US Small Cap Growth” (-1,11%), mentre sono aumentati per le classi “US Large Cap Value” (+6,66%) e “US Small Cap Value” (+1,17%).
- Aumentano i pesi della classe “Mercati Emergenti” (+6,42%).
- Diminiuscono i pesi per la classe “Intl Developed ex-US Market” (-7,17%).
- I pesi per le restanti due classi di attività “Obbligazioni globali (unhedged)” e “Mercato obbligazionario statunitense totale” sono rimasti praticamente identici.
Di seguito è riportata una visualizzazione dei vari pesi delle corrispondenti classi di asset:
- Il modello Black-Litterman (che incorpora le 3 viste).
- I pesi in base alla capitalizzazione di mercato.
- Il modello Media-Varianza (usando i rendimenti medi storici come input).
import matplotlib.pyplot as plt
N = BL_weights_vector.shape[0]
fig, ax = plt.subplots(figsize=(15, 7))
ax.set_title('Black-Litterman Model Portfolio Weights Recommendation vs the Market Portfolio vs Mean-Variance Weights')
ax.plot(np.arange(N)+1, MV_weights_vector, '^', c='b', label='Mean-Variance)')
ax.plot(np.arange(N)+1, asset_weights, 'o', c='g', label='Market Portfolio)')
ax.plot(np.arange(N)+1, BL_weights_vector, '*', c='r',markersize=10, label='Black-Litterman')
ax.vlines(np.arange(N)+1, 0, BL_weights_vector, lw=1)
ax.vlines(np.arange(N)+1, 0, MV_weights_vector, lw=1)
ax.vlines(np.arange(N)+1, 0, asset_weights, lw=1)
ax.axhline(0, c='m')
ax.axhline(-1, c='m', ls='--')
ax.axhline(1, c='m', ls='--')
ax.set_xlabel('Assets')
ax.set_xlabel('Portfolio Weighting')
ax.xaxis.set_ticks(np.arange(1, N+1, 1))
ax.set_xticklabels(asset_weights.index.values)
plt.xticks(rotation=90, )
plt.legend(numpoints=1, fontsize=11)
plt.show()
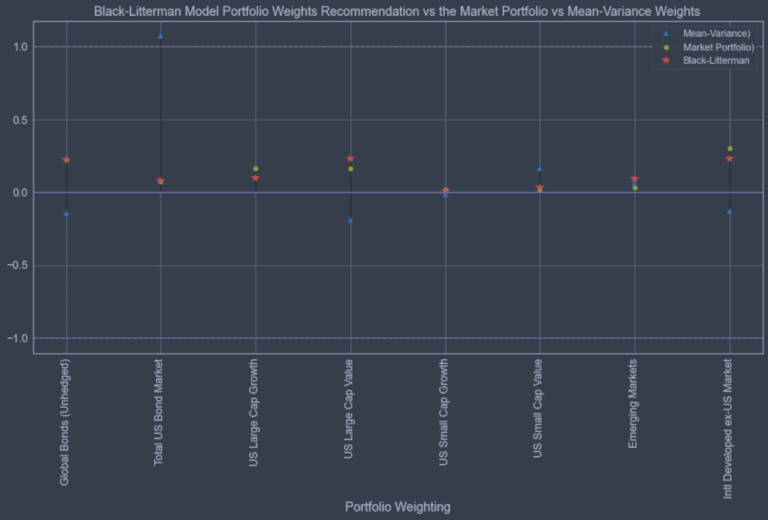
Notiamo che i pesi del modello media-varianza hanno allocazioni molto più “estreme” (ad esempio, pesi superiore al 100% in obbligazioni statunitensi e posizioni short nelle obbligazioni globali, large cap value statunitensi e mercati dei paesi sviluppati internazionali ex-USA).
Uso della libreria Mlfinlab
Possiamo infine rieseguire il modello che abbiamo appena esaminato, utilizzando un a libreria di terze parti chiamata mlfinlab. L’approccio in questo caso prevede di eseguire una rapida convalida dei risultati e tentare di verificarne la correttezza confrontandoli con i risultati ottenuti tramite il modulo “mlfinlab”. Inoltre vogliamo evidenziare e sottolineare che esistono già una serie di librerie Python di terze parti ben documentate che implementano i concetti finanziari classici di asset management e i modelli di asset allocation. Queste librerie offrono una gamma di classi correlate e funzionalità, tutte disponibili per il download e l’utilizzo tramite il comando “pip install”.
Non abbiamo usato una libreria precostruita per l’analisi precedenti al fine di mostrare i passaggi e la logica di applicazione del modello. Le librerie di terzi parti possono “nascondere” molta complessità dietro un’API di alto livello che può consentire la creazione e l’applicazione di vari modelli/classi/metodi/funzioni in un riga o due di codice. Vogliamo invece mostrare come applicare i concetti passo dopo passo perchè è più utile per capire ed imparare questi concetti.
Vediamo quindi come usare mlfinlab per rieseguire l’analisi precedente: non entriamo nei dettagli ma mostriamo solo un output con cui confrontare i risultati precedenti.
Per chi desidera maggiori informazioni sulla libreria e sul modello, può consultare la documentazione ufficiale.
from mlfinlab.portfolio_optimization.bayesian import VanillaBlackLitterman
views = [0.0925, 0.005, 0.055]
pick_list = [
{"Emerging Markets": 1.0},
{"US Large Cap Growth": 0.85,
"US Large Cap Value": -0.85,
"US Small Cap Growth": 0.15,
"US Small Cap Value": -0.15},
{"Intl Developed ex-US Market": 1.0}]
bl = VanillaBlackLitterman()
bl.allocate(covariance=cov,
market_capitalised_weights=asset_weights,
investor_views=views,
pick_list=pick_list,
asset_names=cov.columns,
tau=tau,
risk_aversion=risk_aversion)
Il vettore dei rendimenti di equilibrio impliciti generato dal modello è mostrato di seguito. Possiamo vedere che i valori sono identici al vettore dei rendimenti di equilibrio impliciti che abbiamo generato in precedenza.
print(bl.implied_equilibrium_returns.T)
Global Bonds (Unhedged) 0.012871
Total US Bond Market 0.002439
US Large Cap Growth 0.060436
US Large Cap Value 0.051548
US Small Cap Growth 0.056798
US Small Cap Value 0.043902
Emerging Markets 0.076184
Intl Developed ex-US Market 0.063076
Il vettore dei rendimenti Black-Litterman a posteriori generato dal modello è mostrato di seguito. Possiamo vedere che i valori sono identici al vettore dei rendimenti Black-Litterman che abbiamo generato in precedenza.
print(bl.posterior_expected_returns.T)
Global Bonds (Unhedged) 0.013157
Total US Bond Market 0.002431
US Large Cap Growth 0.057505
US Large Cap Value 0.050891
US Small Cap Growth 0.056636
US Small Cap Value 0.044942
Emerging Markets 0.079098
Intl Developed ex-US Market 0.062403
Il vettore dei pesi del portafoglio consigliati da Black-Litterman, generato dal modello è mostrato di seguito. In questo caso possiamo vedere che ci sono alcune piccole differenze nei valori rispetto ai pesi di portafoglio consigliati da Black-Litterman precedentemente calcolati. Ho incluso di seguito i pesi precedenti per facilitare il confronto. La variazione maggiore riscontrata in tutte le classi di asset è solo dello 0,4%. Probabilmente questa differenza deriva dall’uso della matrice di covarianza originale dei rendimenti in eccesso nel calcolo delle nuove ponderazioni, piuttosto che dalla creazione e l’uso di una matrice di covarianza “posteriore” aggiornata come nel modello mlfinlab.
Per farla breve, sono soddisfatto che i nostri risultati precedenti siano stati confermati come corretti.
weights_table2 = pd.concat([bl.weights.T[0], BL_weights_vector], axis=1) * 100
weights_table2.columns = ['mlfinlab', 'Initial Results']
weights_table2['Difference'] = weights_table2['Initial Results'] - weights_table2['mlfinlab']
weights_table2.style.format('{:,.2f}%')
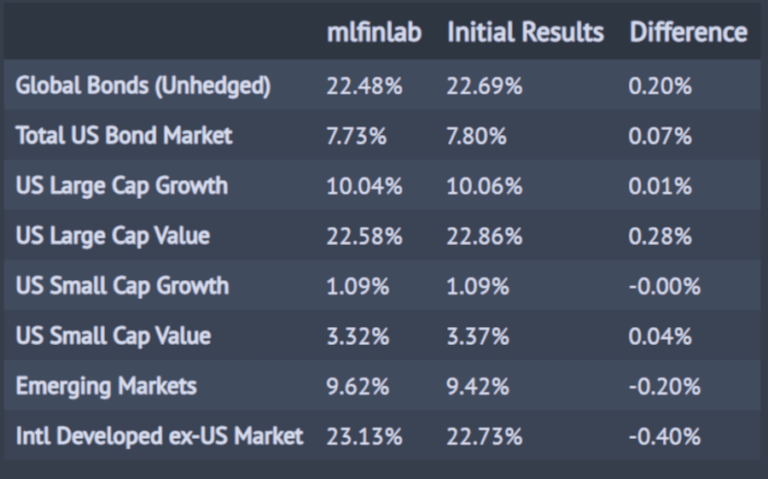
Codice completo
In questo articolo abbiamo descritto come implementare un asset allocation tramite modello di Black-Litterman in Python. Per il codice completo riportato in questo articolo, si può consultare il seguente repository di github:
https://github.com/datatrading-info/Asset_Management