Continuando ad approfondire il tema dell’articolo precedente che descrive una strategia mean-reveting con timeframe intraday, in questo articolo espandiamo il concetto ad un backtest di una strategia mean-reverting short-selling con Python, sempre con timeframe intraday. La strategia prevede, oltre ad acquistare azioni che hanno registrato un gap al ribasso, di vendere allo scoperto azioni che hanno registrato un gap al rialzo.
Vogliamo verificare come lo short-selling influenza i rendimenti e lo Sharpe Ratio. Solitamente c’è una maggiore inefficienza sul lato short del mercato a causa di vari aspetti (ad esempio, l’incapacità dei grandi fondi pensione di vendere azioni allo scoperto a causa delle restrizioni del mandato di investimento).
Questa maggiore inefficienza del mercato dovrebbe teoricamente portare a rendimenti più elevati per gli operatori che sono in grado di sfruttare le opportunità di short-selling.
Iniziamo il backtesting con lo stesso universo di titoli azionari usato nell’articolo precedente. L’elenco dei titoli azionari NSYE può essere scaricato al seguente link: NYSE.txt.
Il codice
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
import yfinance as yf
from math import sqrt
# Assicurara che il file NYSE.txt sia nella stessa cartella dello script
stocks = pd.read_csv('NYSE.txt',delimiter="\t")
# Creao una lista vuota per i ticker azionari
stocks_list = []
# Iterazione tramite il dataframe pandas e aggiunta dei ticker nella lista
for symbol in stocks['Symbol']:
stocks_list.append(symbol)
# Crea una lista vuota
frames = []
for stock in stocks_list:
try:
# Download dei dati delle azioni in DataFrame
df = yf.download(stock, start='2000-01-01', end='2020-01-01')
# Crea la deviazione standard mobile a 90 giorni
df['Stdev'] = df['Close'].rolling(window=90).std()
# Crea la media mobile a 20 giorni
df['Moving Average'] = df['Close'].rolling(window=20).mean()
# Verifica se il gap tra il minimo precedente e l'apertura
# odierna è maggiore della deviazione standard a 90 giorni
df['Buy1'] = (df['Open'] - df['Low'].shift(1)) < -df['Stdev']
# Verifica se il prezzo di apertura è maggiore della media mobile a 20 giorni
df['Buy2'] = df['Open'] > df['Moving Average']
# Segnale BUY se entrambi i criteri sono veri
df['BUY'] = df['Buy1'] & df['Buy2']
# Verifica che il gap tra il massimo precedente e l'apertura
# odierna è maggiore della deviazione standard a 90 giorni
df['Sell1'] = (df['Open'] - df['High'].shift(1)) > df['Stdev']
# Verifica se il prezzo di apertura è minore della media mobile a 20 giorni
df['Sell2'] = df['Open'] < df['Moving Average']
# Segnale SELL se entrambi i criteri sono veri
df['SELL'] = df['Sell1'] & df['Sell2']
# Calcola i rendimenti giornalieri percentuali delle azioni
df['Pct Change'] = (df['Close'] - df['Open']) / df['Open']
# Redimenti della strategia usando i rendimenti giornalieri delle
# azioni quando abbiamo un segnale BUY
df['Rets'] = df['Pct Change'][df['BUY'] == True]
# Rendimenti della strategia usando i rendimenti giornalieri del titolo
# moltiplicati per 1 se siamo long e -1 se siamo short
df['Rets'] = np.where(df['BUY'],df['Pct Change'], 0)
df['Rets'] = np.where(df['SELL'],-df['Pct Change'], df['Rets'])
# Aggiungere il rendimento della strategia alla lista
frames.append(df['Rets'])
except:
pass
# Concate i singoli dataframe della nostra lista lungo l'asse delle colonne
masterFrame = pd.concat(frames,axis=1)
# Crea la somma dei rendimenti giornalieri delle singole strategie
masterFrame['Total'] = masterFrame.sum(axis=1)
masterFrame.fillna(0,inplace=True)
# Conteggia il numero di titoli che sono tradate ogni giorno
masterFrame['Count'] = (masterFrame != 0).sum(axis=1) - 1
# Divide il rendimenti giornalieri "totali" per il numero di titoli che sono
# tradati ogni giorno per ottenere i rendimenti equamente pesati.
masterFrame['Return'] = masterFrame['Total'] / masterFrame['Count']
masterFrame['Return'].dropna().cumsum().plot()
plt.show()
SharpeRatio = (masterFrame['Return'].mean() *252) / (masterFrame['Return'].std() * (sqrt(252)))
print(SharpeRatio)
Annual_Return = (masterFrame['Return'].dropna().cumsum()[-1]+1)**(365.0/252) - 1
print(Annual_Return)
Il Risultato
Otteniamo la seguente curva equity
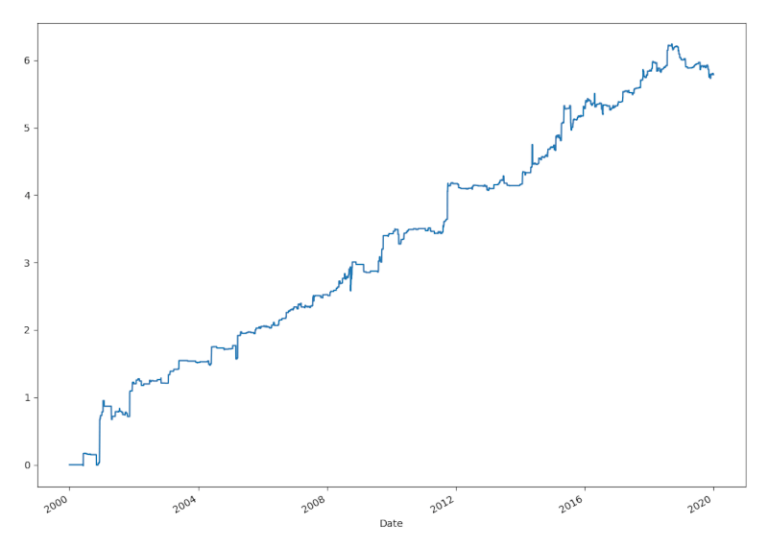
con un rapporto di Sharpe e un rendimento annuo pari a
0.8253678556298382
15.014375433065773
Vediamo che dopo aver aggiunto il lato short della strategia lo Sharpe Ratio è diminuito a 0,8 mentre il rendimento annuo è aumentato al 15%.
Per valutare la strategia dipende da quale parametro è più importante per te, il rendimento diretto o rendimento corretto per il rischio. E’ una tua scelta personale!
Backtest nel mercato italiano
Solo per un po’ di curiosità, eseguiamo questa strategia su un altro universo di investimento di azioni, questa volta i ticker della Borsa Italiana (MIB).
L’elenco può essere scaricato al seguente link: MIB.txt.
Eseguendo il backtest otteniamo la seguente curva di equity.
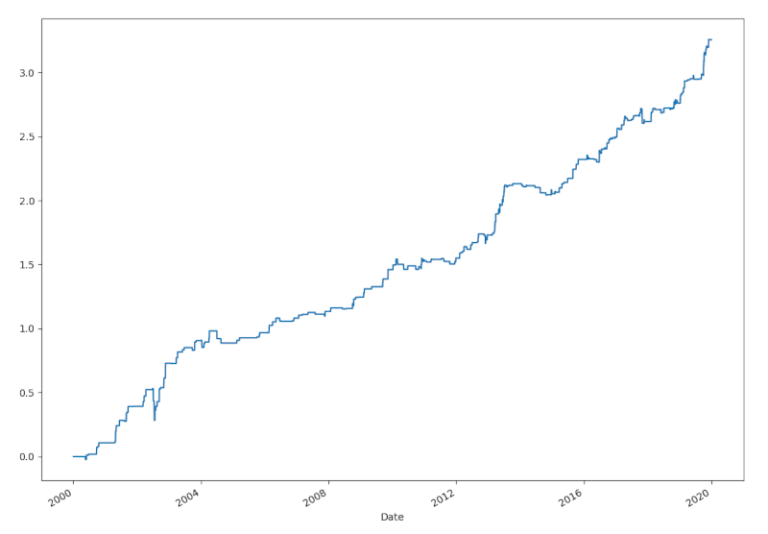
con uno Sharpe Ratio di 1.398 e un rendimento annuo del 714,5 non è male per un mercato che ha sottoperformato rispetto al mercato statunitense nel periodo considerato.
Sebbene i risultati di questi mercati sembrino molto promettenti, bisogna fare attenzione quando si vuole provare questa strategia nel trading dal vivo. E’ molto verosimile che molti dei titoli venduto allo scoperto dalla strategia non sarebbero effettivamente disponibili per lo short nel mercato live e i costi di transazione sarebbero abbastanza alti da assorbire gran parte dei rendimenti.
Ad ogni modo, è comunque divertente indagare su queste cose ed avere un’idea di base per iniziare ulteriori ricerche per ottenere una strategia redditizia.
Codice completo
In questo articolo abbiamo descritto come implementare il backtest di una strategia mean-reverting short-selling con Python. Per il codice completo riportato in questo articolo, si può consultare il seguente repository di github:
https://github.com/datatrading-info/Backtest_Strategie





