In questo articolo descriviamo come calcolare la Skewness e la Kurtosis con Python, cioè l’assimetria e la curtosi di una serie finanziaria. In altre parole vogliamo analizzare una serie di rendimenti calcolando le caratteristiche statistiche come la media, la varianza e quindi l’assimetria e la curtosi.
La skewness e la kurtosis
Quando analizziamo i rendimenti di una serie finanziaria, ci concentriamo sui primi 2 ‘momenti’ della distribuzione; cioè la media e la varianza dei rendimenti. La media rappresenta il rendimento medio atteso mentre la varianza misura la dispersione dei rendimenti attorno alla media. Queste due misure non fornisco però il quadro completo. Ci sono momenti di “ordine superiore” che dobbiamo considerare…
La skewness (cioè l’asimmetria) misura la simmetria di una distribuzione. Un set di dati simmetrico ha un’asimmetria pari a 0, quindi una distribuzione normale ha un’asimmetria pari a 0. La skewness misura essenzialmente la dimensione relativa delle due code.
La kurtosis (cioè la curtosi) misura lo “spessore” delle code di una funzione di densità, ovvero il grado di “appiattimento” di una distribuzione. L’interesse per questo indice è dato dal fatto che lo “spessore” delle code influenza il comportamento di diverse statistiche. Il valore viene spesso confrontato con la curtosi della distribuzione normale, che è pari a 3. Se la curtosi è maggiore di 3, il set di dati ha code più pesanti rispetto a una distribuzione normale (più code). Se la curtosi è inferiore a 3, il set di dati ha code più leggere rispetto a una distribuzione normale (meno code). La curtosi è talvolta segnalata come “curtosi in eccesso”. L’eccesso di curtosi è determinato sottraendo 3 dalla curtosi. Ciò rende la curtosi della distribuzione normale uguale a 0.
Implementazione con Python
Dopo avere descritto le funzioni basi di Pandas nel precedente articolo, vediamo ora come calcolare la skewness e la kurtosis con Python per analizzare una serie di rendimenti. Usiamo Yfinance per scaricare i prezzi storici di Google e quindi usiamo Pandas per trasformare la serie di prezzi in una serie di rendimenti percentuali giornalieri.
Innanzitutto, dobbiamo importare il relativo modulo yfinance e quindi usare la funzione download per scaricare la cronologia dei prezzi di Google da Yahoo Finance a partire dal 01/01/2000. Quindi usiamo il metodo .head() per mostrare le prime 5 righe del DataFrame che contiene i dati dei prezzi di Google.
import pandas as pd
import yfinance as yf
GOOG = yf.download('GOOG', start='2000-01-01', end='2020-01-01')
print(GOOG.head())
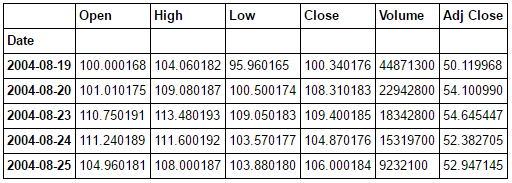
.head() per stampare i valori calcolati, come segue:
GOOG['Percentage Returns'] = GOOG['Adj Close'].pct_change()
print(GOOG.head())
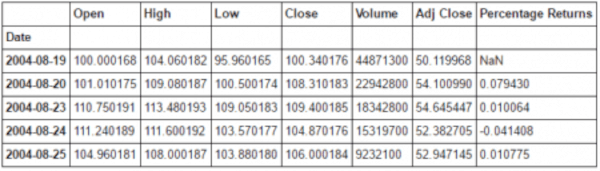
Possiamo vedere che il DataFrame contiene la colonna “Percentage Returns”. Usiamo questa colonna per tracciare l‘istogramma dei rendimenti e visualizzare la forma della distribuzione
GOOG['Percentage Returns'].plot(kind='hist',bins=100)
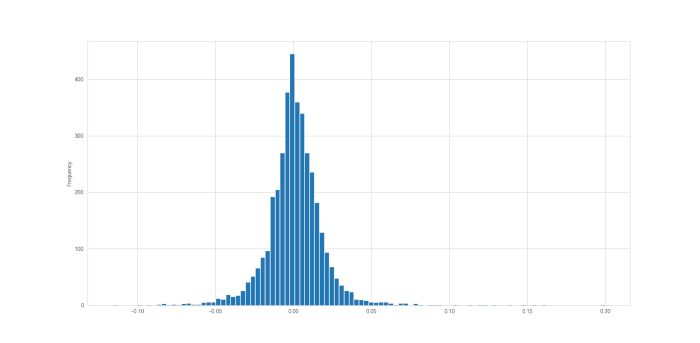
Quindi possiamo rapidamente verificare i primi due momenti (media e varianza) della distribuzione usando i seguenti comandi:
print('Mean =:',GOOG['Percentage Returns'].mean())
print('Variance =:',GOOG['Percentage Returns'].var())
Mean =: 0.0010267544346467274
Variance =: 0.00035714327152804634
Quindi, a prima vista, la distribuzione sembra “normale”, anche se un po’ più alta e con code più grosse di quanto ci si aspetterebbe da una distribuzione veramente normale. Vediamo se riusciamo a sovrapporre un grafico di una distribuzione normale effettiva, con la stessa media e varianza a quella restituita da Google per effettuare più facilmente il confronto.
import matplotlib.pyplot as plt
import numpy as np
import scipy.stats as stats
# Converte il dataframe pandas in un array numpy array e lo ordina
h = np.asarray(GOOG['Percentage Returns'].dropna())
h = sorted(h)
# usa il modulo stats di scipy per allenare una distribuzione normale con stessa media e deviazione standard
fit = stats.norm.pdf(h, np.mean(h), np.std(h))
# Grafico dell'istogramma di entrambe le serie
plt.plot(h, fit, '-', linewidth=2)
plt.hist(h, normed=True, bins=100)
plt.show()
print("")
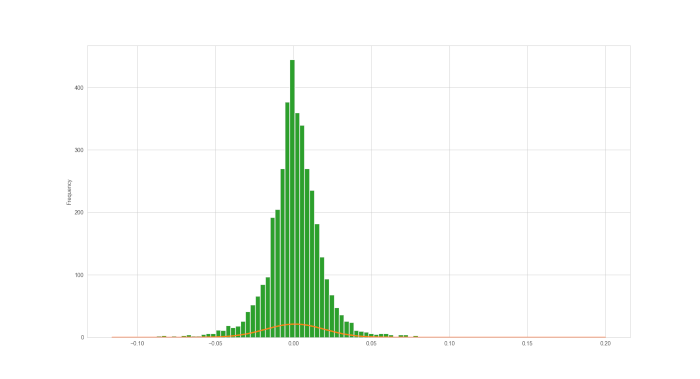
Vediamo come le nostre ipotesi sono confermate. Abbiamo un eccesso di curtosi, ma è difficile dire se abbiamo qualche asimmetria.
Per avere una conferma possiamo calcolare i valori di skewness e kurtosis:
print('Skew =', GOOG['Percentage Returns'].skew())
print('Kurtosis =', GOOG['Percentage Returns'].kurt())
Skew = 0.907067745521419
Kurtosis = 11.554186118472607
Sottolineiamo che la funzione kurt() di Pandas restituisce la curtosi imparziale sull’asse richiesto usando la definizione di curtosi di Fisher (curtosi del normale == 0.0) normalizzata da N-1″, quindi questo valore corrisponde al “Eccesso curtosi”.
Abbiamo verificato che la distribuzione dei rendimenti di Google una significativa curtosi in eccesso ed è leggermente distorta positivamente.
Codice completo
In questo articolo abbiamo descritto come calcolare la Skewness e la Kurtosis con Python. Per il codice completo riportato in questo articolo, si può consultare il seguente repository di github:
https://github.com/datatrading-info/AnalisiDatiFinanziari