In questo articolo descriviamo e confrontiamo alcuni metodi per ottimizzare l’asset allocation di un portafoglio di investimenti con Python. In particolare usiamo l’algoritimo di Monte Carlo, l’ottimizzazione in stile “forza bruta” e la funzione optimize di Scipy per “minimizzare (o massimizzare) le funzioni obiettivo, possibilmente soggetti a vincoli”, come si legge nella documentazione ufficiale.
Questo articolo continua ed approfondisce i concetti e gli approcci introdotti nel precedente articolo sull’ottimizzazione di un portafoglio di investimenti con Python.
Per introdurre i metodi di ottimizzazione consideriamo un portafoglio di azioni, e desideriamo bilanciare/ribilanciare gli asset in modo da avere i pesi “ottimali”. Come descritto nell’articolo precedente, un portafoglio “ottimale” è il portafoglio con lo Sharpe Ratio maggiore, noto come portafoglio “con media-varianza ottimale”.
Ottimizzazione dello Sharpe Ratio
Il primo metodo che possiamo applicare per ottimizzare l’asset allocation di un portafoglio di investimenti è un approccio Monte Carlo in stile “forza bruta”. Con questo approccio cerchiamo di ricavare i pesi ottimali creando un gran numero di portafogli casuali, tutti con diverse combinazioni di pesi degli asset che compongo il portafoglio. Calcoliamo e memorizziamo lo Sharpe Ratio di ogni portafoglio con pesi casuale e quindi ricavare i pesi del portafoglio corrispondente allo Sharpe Ratio più alto.
I pesi casuali che creiamo in questo esempio hanno alcuni vincoli. Il peso di ogni asset deve essere compreso tra zero e uno e, inoltre, la somma di tutti i pesi deve essere pari a uno per rappresentare un investimento del 100% del capitale teorico.
Più portafogli casuali creiamo e, teoricamente, più ci avviciniamo ai pesi ottimali del portafoglio “reale”. Tuttavia, otteniamo sempre alcune approssimazioni e stime perchè non potremo mai eseguire abbastanza portafogli simulati per individuare i pesi “perfetti” che stiamo cercando. Possiamo avvicinarci, ma mai esatti.
In questo esempio descriviamo come creare un portafoglio di 5 azioni ed eseguire 100.000 simulazioni di portafogli per individuare i pesi ottimali. Produciamo quindi un grafico con i valori di tutti i portafogli dove evidenziamo il portafoglio “ottimale” con lo Sharpe Ratio più alto e il “portafoglio a varianza minima”. Il “portafoglio a varianza minima” è, come dice il nome, il portafoglio con la varianza più bassa che, per definizione, identifica anche la deviazione standard o “volatilità” più bassa.
Il codice
Iniziamo con importare le librerie necessarie
import pandas as pd
import numpy as np
import yfinance as yf
import datetime
import scipy.optimize as sco
from scipy import stats
import matplotlib.pyplot as plt
Scarichiamo i dati storici dei prezzi delle azioni che vogliamo includere nel portafoglio. In questo esempio usiamo 5 titoli azionari che tutti i trader conoscono. Apple, Microsoft, Netflix, Amazon e Google.
tickers = ['AAPL', 'MSFT', 'NFLX', 'AMZN', 'GOOG']
start = '2010-01-01'
end = '2020-01-01'
df = pd.DataFrame([yf.download(ticker, start, end)['Adj Close'] for ticker in tickers]).T
df.columns = tickers
Per produrre i risultati dell’ottimizzazione implementiamo due funzioni. La prima funzione calc_portfolio_perf calcola il rendimento annualizzato, la deviazione standard annualizzata e lo Sharpe Ratio annualizzato di ogni portafoglio, a partire dai parametri in ingresso. I parametri della funzione sono i pesi degli asset del portafoglio, il rendimento giornaliero medio di ogni asset (calcolato dati dati storici che abbiamo scaricato, la matrice di covarianza degli asset e infine il tasso di interesse della componente risk free. Il free risk rate è usato per calcolare lo Sharpe Ratio ed è definito su base annua. In questo esempio impostiamo un free risk rate pari a zero per semplicità, ma abbiamo implementato la logica in modo da poter facilmente modificare i parametri.
La seconda funzione simulate_random_portfolios permette la creazione di più portafogli pesati in modo casuale, che sono usati come input per la prima funzione per calcolare e memorizzare i valori richiesti dall’ottimizzazione. Dopo aver simulato tutti i portafogli, i risultati sono archiviati e restituiti come Pandas DataFrame.
Come accennato in precedenza, memorizziamo i valori del rendimento annualizzato, la deviazione standard annualizzata e lo Sharpe Ratio annualizzato. Memorizziamo anche i pesi di ciascun titolo nel portafoglio che hanno generato tali valori.
def calc_portfolio_perf(weights, mean_returns, cov, rf):
portfolio_return = np.sum(mean_returns * weights) * 252
portfolio_std = np.sqrt(np.dot(weights.T, np.dot(cov, weights))) * np.sqrt(252)
sharpe_ratio = (portfolio_return - rf) / portfolio_std
return portfolio_return, portfolio_std, sharpe_ratio
def simulate_random_portfolios(num_portfolios, mean_returns, cov, rf):
results_matrix = np.zeros((len(mean_returns) + 3, num_portfolios))
for i in range(num_portfolios):
weights = np.random.random(len(mean_returns))
weights /= np.sum(weights)
portfolio_return, portfolio_std, sharpe_ratio = calc_portfolio_perf(weights, mean_returns, cov, rf)
results_matrix[0, i] = portfolio_return
results_matrix[1, i] = portfolio_std
results_matrix[2, i] = sharpe_ratio
for j in range(len(weights)):
results_matrix[j + 3, i] = weights[j]
results_df = pd.DataFrame(results_matrix.T, columns=['ret', 'stdev', 'sharpe'] + [ticker for ticker in tickers])
return results_df
simulate_random_portfolios e memorizziamo i risultati in una variabile in modo da poterli estrarre e visualizzare.
mean_returns = df.pct_change().mean()
cov = df.pct_change().cov()
num_portfolios = 100000
rf = 0.0
results_frame = simulate_random_portfolios(num_portfolios, mean_returns, cov, rf)
Possiamo visualizzare i risultati di tutti i portafogli simulati in un grafico. Per ogni portafoglio riportiamo il valore del rendimento annualizzato sull’asse y e la volatilità annualizzata sull’asse x. Evidenziamo inoltre i 2 portafogli “ottimali”. Il portafoglio con lo Sharpe Ratio maggiore è evidenziato con una stella rossa mentre il portafoglio con varianza minima tramite una stella verde.
I singoli portafogli sono colorati in base ai rispettivi Sharpe RAtio. Il blu indica un valore più alto e il rosso un valore più basso.
# Indentifica il portafoglio con lo Sharpe Ratio più alto
max_sharpe_port = results_frame.iloc[results_frame['sharpe'].idxmax()]
# Identifica il portafoglio con la deviazione standard più piccola
min_vol_port = results_frame.iloc[results_frame['stdev'].idxmin()]
# Crea il grafico scatter colorato in base allo Sharpe Ratio
plt.subplots(figsize=(15,10))
plt.scatter(results_frame.stdev,results_frame.ret,c=results_frame.sharpe,cmap='RdYlBu')
plt.xlabel('Standard Deviation')
plt.ylabel('Returns')
plt.colorbar()
# Visualizza una stella rossa per il portafoglio con lo Sharpe Ratio più alto
plt.scatter(max_sharpe_port[1],max_sharpe_port[0],marker=(5,1,0),color='r',s=500)
# Visualizza una stella verda per il portafoglio con la deviazione standard più piccola
plt.scatter(min_vol_port[1],min_vol_port[0],marker=(5,1,0),color='g',s=500)
plt.show()
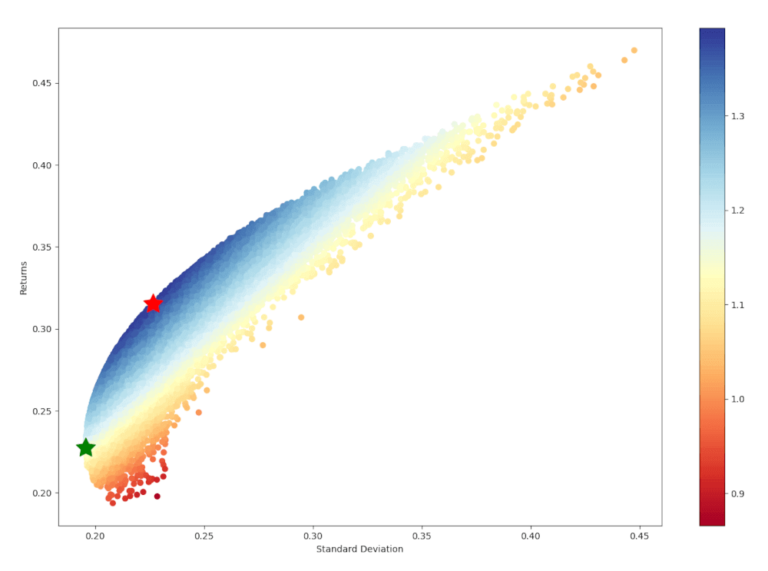
Verifichiamo i pesi degli asset azionari calcolati per questi due portafoglio, insieme al rendimento annualizzato, alla deviazione standard annualizzata e allo Sharpe Ratio annualizzato. Di seguito vediamo questi valori per il portafoglio con lo Sharpe Ratio massimo e il portafoglio con la varianza minima.
print(max_sharpe_port.to_frame().T)

print(min_vol_port.to_frame().T)

Ottimizzazione con l’algoritmo SLSQP
Vediamo ora un secondo approccio per ottimizzare l’asset allocation di un portafoglio di investimenti, che usa le funzioni di optimize di Scipy. Il codice è abbastanza breve ma ci sono un paio di cose da sottolineare. In primo luogo, la libreria Scipy offre una funzione di “minimizzazione”, ma nessuna funzione di “massimizzazione”. Dato che vogliamo massimizzare il rapporto di Sharpe, a prima vista questo può sembrare un problema. Si risolve facilmente considerando che la massimizzazione dello Sharpe Ratio è analoga alla minimizzazione del negativo dello Sharpe Ratio.
Definiamo una funzione (molto simile alla funzione precedente) che calcola e restituisce il negativo dello Sharpe Ratio di un portafoglio. Quindi definiamo una variabile chiamata constraints. Questo può sembrare un po’ strano se non hai mai usato le funzionalità di “ottimizzazione” di Scipy.
Dato che nella nostra funzione minimize usiamo il metodo SLSQP (Sequential Least Squares Programming), il parametro l’argomento constraints deve essere una lista elenco di dizionari. I dizionari devono contenere i campi type e fun, e facoltativamente i campi jac e args.
Il campo tipo può avere i valori essere “eq” o “ineq” riferendosi rispettivamente a “uguaglianza” o “ineguaglianza”. Il campo fun si riferisce alla funzione che definisce il vincolo. In questo caso il vincolo prevede che la somma dei pesi degli asset deve essere uno. Il valore “eq” significa che la funzione sia uguale a zero (quindi l’uguaglianza si riferisce effettivamente ad una uguaglianza a zero). Il modo più semplice per raggiungere questo obiettivo è creare una funzione lambda che restituisca la somma dei pesi del portafoglio, meno 1. Il vincolo che la somma deve essere zero (cioè la funzione deve equivalere a zero) per definizione significa che la somma dei pesi deve essere pari a uno.
La variabile bounds permette di definire i “limiti” del peso di ogni singolo peso dello stock compreso tra 0 e 1, ed è inserita all’interno del argomento args come parametro che vogliamo passare alla funzione che stiamo cercando di minimizzare (calc_neg_sharpe).
def calc_neg_sharpe(weights, mean_returns, cov, rf):
portfolio_return = np.sum(mean_returns * weights) * 252
portfolio_std = np.sqrt(np.dot(weights.T, np.dot(cov, weights))) * np.sqrt(252)
sharpe_ratio = (portfolio_return - rf) / portfolio_std
return -sharpe_ratio
def max_sharpe_ratio(mean_returns, cov, rf):
num_assets = len(mean_returns)
args = (mean_returns, cov, rf)
constraints = ({'type': 'eq', 'fun': lambda x: np.sum(x) - 1})
bound = (0.0,1.0)
bounds = tuple(bound for asset in range(num_assets))
result = sco.minimize(calc_neg_sharpe, num_assets*[1./num_assets,], args=args, method='SLSQP', bounds=bounds, constraints=constraints)
return result
mean_returns = df.pct_change().mean()
cov = df.pct_change().cov()
num_portfolios = 100000
rf = 0.0
optimal_port_sharpe = max_sharpe_ratio(mean_returns, cov, rf)
Quando eseguiamo l’ottimizzazione, otteniamo i seguenti risultati.
print(pd.DataFrame([round(x,2) for x in optimal_port_sharpe['x']],index=tickers).T)

Se confrontiamo questi risultati con quelli dell’approccio Monte Carlo, possiamo vedere che sono simili, ma ovviamente non saranno identici. I pesi di ciascun titolo tra i due approci non si differenziamo per più di un paio di punti percentuali.
Possiamo usare lo stesso approccio per identificare il portafoglio con varianza minore. Il codice è quasi identico al precedente con la sola differenza che in questo caso abbiamo bisogno di una funzione calc_portfolio_std per calcolare e restituire la volatità di un portafoglio, e usarla come funzione che vogliamo minimizzare. In questo caso non è necessario negare l’output della funzione perchè dobbiamo trovare il risultato minimo (al contrario dello Sharpe Ratio dove volevamo trovare il massimo)
I vincoli rimangono gli stessi. Adattiamo la precedente funzione max_sharpe_ratio, rinominiamola in min_variance e cambiamo la variabile args per contenere gli argomenti corretti che dobbiamo passare alla funzione calc_portfolio_std che vogliamo minimizzare.
def calc_portfolio_std(weights, mean_returns, cov):
portfolio_std = np.sqrt(np.dot(weights.T, np.dot(cov, weights))) * np.sqrt(252)
return portfolio_std
def min_variance(mean_returns, cov):
num_assets = len(mean_returns)
args = (mean_returns, cov)
constraints = ({'type': 'eq', 'fun': lambda x: np.sum(x) - 1})
bound = (0.0,1.0)
bounds = tuple(bound for asset in range(num_assets))
result = sco.minimize(calc_portfolio_std, num_assets*[1./num_assets,], args=args, method='SLSQP', bounds=bounds, constraints=constraints)
return result
min_port_variance = min_variance(mean_returns, cov)
Eseguendo l’ottimizzazione, otteniamo i seguenti risultati.
print(pd.DataFrame([round(x,2) for x in min_port_variance['x']],index=tickers).T)

Anche in questo caso vediamo che i risultati sono molto vicini a quelli che abbiamo ottenuto usando l’approccio Monte Carlo.
Ottimizzazione del Value at Risk (VaR)
Vediamo ora un altro approccio per ottimizzare l’asset allocation di un portafoglio di investimenti, individuando i pesi del portafoglio che minimizzano il Value at Risk (VaR). La logica è molto simile a quella prevista per l’approccio Monte Carlo, quindi evidenziamo solo le integrazione e le differente.
Creiamo le due funzioni. In questo caso invece di restituire il rendimento del portafoglio, la volatilità e lo Sharpe Ratio, calcoliamo restituiamo il VaR parametrico del portafoglio per uno specifico livello di confidenza determinato dal valore del parametro alfa e ad una scala temporale determinata dal parametro days.
Per calcolare il vaR usiamo il metodo che prevede di scalare la deviazione standard del portafoglio per la radice quadrata del valore di <code<days. Inoltre scaliamo linearmente i rendimenti giornalieri medi del portafoglio in base al valore di days. Quindi moltiplichiamo la deviazione standard scalata per il relativo Z value in base al valore di alfa” per i rendimenti giornalieri medi scalati. Converiamo poi questo valore del VaR in un valore assoluto, poiché il VaR è spesso riportato come valore positivo. In questo modo possiamo anche di eseguire la funzione di “minimizzazione” richiesta quando il VaR è espresso come valore positivo.
Sottolineiamo che il VaR è a volte calcolato in modo che i rendimenti medi del portafoglio siano considerati sufficientemente piccoli da poter essere inseriti nell’equazione con un valore nullo. Questo ha senso quando guardiamo al VaR su periodi di tempo brevi come intervalli giornalieri o settimanali. Tuttavia quando consideriamo il VaR annualizzato ha senso prevedere un elemento di rendimento “diverso da zero”.
Inserire rendimenti nullo, rimuovendoli di fatto dal calcolo, è talvolta preferito perchè è una stima più “pessimistica” del VaR di un portafoglio e quando si tratta di quantificare il rischio, o di fatto qualsiasi “ribasso” è saggio peccare di prudenza e prendere decisioni basate sullo scenario peggiore. Il costo dell’errore dovuto alla sottostima del VaR e quello dovuto alla sovrastima del VaR non è quasi mai simmetrico. Abbiamo quasi sempre un costo maggiore per una sottostima.
La seconda funzione è praticamente analoga a quella usata per l’ottimizzazione dello Sharpe Ratio con alcune lievi modifiche ai nomi delle variabili, ai parametri e agli argomenti passati.
def calc_portfolio_perf_VaR(weights, mean_returns, cov, alpha, days):
portfolio_return = np.sum(mean_returns * weights) * days
portfolio_std = np.sqrt(np.dot(weights.T, np.dot(cov, weights))) * np.sqrt(days)
portfolio_var = abs(portfolio_return - (portfolio_std * stats.norm.ppf(1 - alpha)))
return portfolio_return, portfolio_std, portfolio_var
def simulate_random_portfolios_VaR(num_portfolios, mean_returns, cov, alpha, days):
results_matrix = np.zeros((len(mean_returns) + 3, num_portfolios))
for i in range(num_portfolios):
weights = np.random.random(len(mean_returns))
weights /= np.sum(weights)
portfolio_return, portfolio_std, portfolio_VaR = calc_portfolio_perf_VaR(weights, mean_returns, cov, alpha, days)
results_matrix[0, i] = portfolio_return
results_matrix[1, i] = portfolio_std
results_matrix[2, i] = portfolio_VaR
for j in range(len(weights)):
results_matrix[j + 3, i] = weights[j]
results_df = pd.DataFrame(results_matrix.T, columns=['ret', 'stdev', 'VaR'] + [ticker for ticker in tickers])
return results_df
La variabile days determina l’intervallo di tempo su cui calcoliamo/scaliamo il VaR e la variabile alfa è il livello di significatività usato il calcolo, con il livello di confidenza pari a (1 – livello di significatività).
Abbiamo 252 giorni per rappresentare i giorni di mercato aperto in un anno e un alfa di 0,05, corrispondente a un livello di confidenza del 95%. In altre parole calcoliamo il VaR del 95% su un anno e cercheremo di minimizzare tale valore.
Ora eseguiamo la funzione di simulazione e visualizziamo i risultati.
mean_returns = df.pct_change().mean()
cov = df.pct_change().cov()
num_portfolios = 100000
rf = 0.0
days = 252
alpha = 0.05
results_frame = simulate_random_portfolios_VaR(num_portfolios, mean_returns, cov, alpha, days)
In questo caso visualizziamo i risultati di ciascun portafoglio con il rendimento annualizzato sull’asse y e il VaR del portafoglio sull’asse x. Il grafico colora i punti dati in base al valore del VaR per quel portafoglio.
# Posizione del portafoglio con il Var minimo
min_VaR_port = results_frame.iloc[results_frame['VaR'].idxmin()]
# Grafico scatter colorato in base al VaR
plt.subplots(figsize=(15,10))
plt.scatter(results_frame.VaR,results_frame.ret,c=results_frame.VaR,cmap='RdYlBu')
plt.xlabel('Value at Risk')
plt.ylabel('Returns')
plt.colorbar()
# Visualizza una stella rossa nella posizione del portafoglio con VaR minimo
plt.scatter(min_VaR_port[2],min_VaR_port[0],marker=(5,1,0),color='r',s=500)
plt.show()
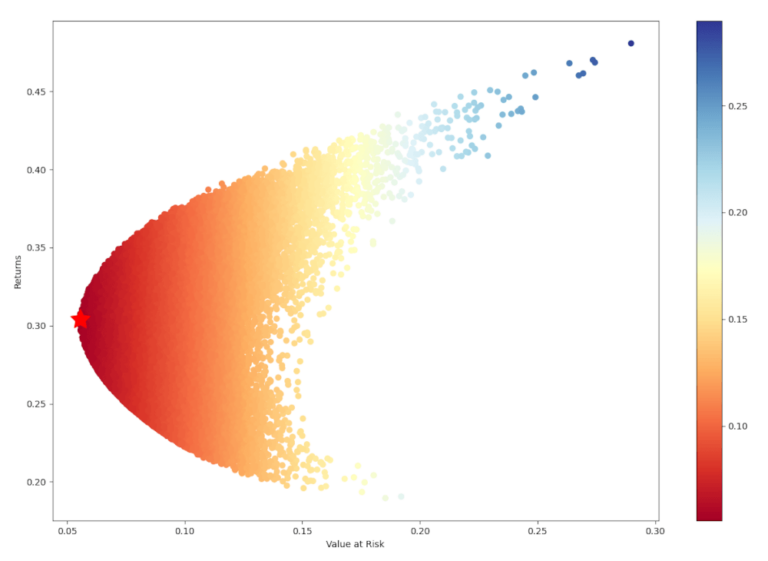
Otteniamo i seguenti pesi per il portafoglio che minimizza il VaR.
print(min_VaR_port.to_frame().T)

Fin qui sembra tutto corretto, ma cosa succede se visualizziamo la posizione del portafoglio con VaR minimo su un grafico con il rendimento sull’asse y e la deviazione standard sull’asse x (in analogia agli approcci precedente). I punti dati sono ancora colorati in base al corrispondente valore del VaR. Diamo un’occhiata.
# Posizione del portafoglio con il Var minimo
min_VaR_port = results_frame.iloc[results_frame['VaR'].idxmin()]
# Grafico scatter colorato in base al VaR
plt.subplots(figsize=(15,10))
plt.scatter(results_frame.stdev,results_frame.ret,c=results_frame.VaR,cmap='RdYlBu')
plt.xlabel('Standard Deviation')
plt.ylabel('Returns')
plt.colorbar()
# Visualizza una stella rossa nella posizione del portafoglio con VaR minimo
plt.scatter(min_VaR_port[1],min_VaR_port[0],marker=(5,1,0),color='r',s=500)
plt.show()
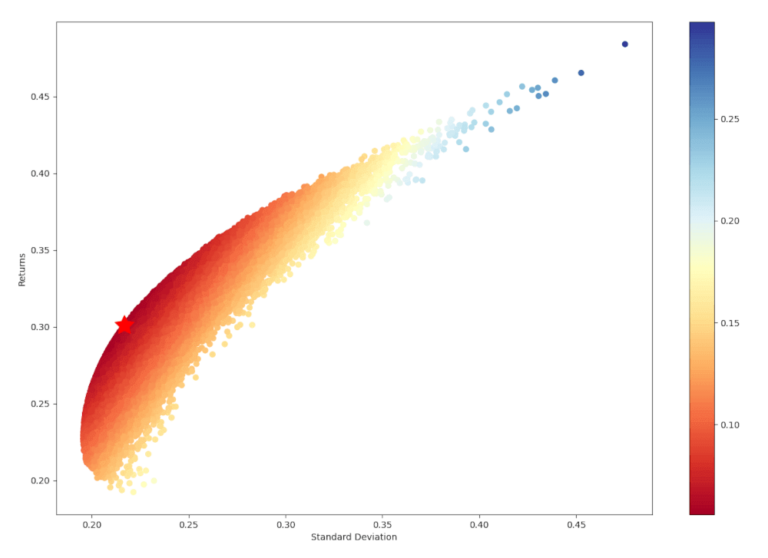
Vediamo che i risultati delle simulazioni del portafoglio con VaR minimo sono molto alle simulazione del portafoglio con Sharpe Ratio massimo. Questo è prevedibile considerando il metodo di calcolo scelto per il VaR.
Il VaR diminuisce quando i rendimenti del portafoglio aumentano e viceversa, mentre lo Sharpe Ratio aumenta all’aumentare dei rendimenti del portafoglio, quindi ciò che minimizza il VaR in termini di rendimenti in realtà massimizza lo Sharpe Ratio.
Allo stesso modo, un aumento della deviazione standard del portafoglio aumenta il VaR ma diminuisce lo Sharpe Ratio, quindi ciò che massimizza il VaR in termini di deviazione standard del portafoglio in realtà minimizzalo Sharpe Ratio.
Quindi cercare il portafolio con il VaR minimo o con lo Sharpe Ratio massimo sono raggiunti con portafogli “simili”.
Passiamo ora al secondo approccio per identificare il portafoglio con VaR minimo. Anche in questo caso il codice è piuttosto simile al codice di ottimizzazione usato per calcolare i portafogli con lo Sharpe Ratio massimo e varianza minima, con qualche piccola modifica.
Abbiamo bisogno di una nuova funzione per calcolare e restituire solo il VaR di un portafoglio. Quindi l’unica differenza con la funzione originale che calcolava il VaR è la restituizione di un singolo valore VaR senza restituire il rendimento del portafoglio e la deviazione standard.
La funzione min_VaR agisce in modo molto simile alle funzioni max_sharpe_ratio e min_variance. Modifichiamo gli argomenti richiesti. I vincoli sono gli stessi, così come i limiti ecc.
def calc_portfolio_VaR(weights, mean_returns, cov, alpha, days):
portfolio_return = np.sum(mean_returns * weights) * days
portfolio_std = np.sqrt(np.dot(weights.T, np.dot(cov, weights))) * np.sqrt(days)
portfolio_var = abs(portfolio_return - (portfolio_std * stats.norm.ppf(1 - alpha)))
return portfolio_var
def min_VaR(mean_returns, cov, alpha, days):
num_assets = len(mean_returns)
args = (mean_returns, cov, alpha, days)
constraints = ({'type': 'eq', 'fun': lambda x: np.sum(x) - 1})
bound = (0.0,1.0)
bounds = tuple(bound for asset in range(num_assets))
result = sco.minimize(calc_portfolio_VaR, num_assets*[1./num_assets,], args=args, method='SLSQP', bounds=bounds, constraints=constraints)
return result
min_port_VaR = min_VaR(mean_returns, cov, alpha, days)
Quando eseguiamo l’ottimizzazione, otteniamo i seguenti risultati.
print(pd.DataFrame([round(x,2) for x in min_port_VaR['x']],index=tickers).T)

Anche in questo caso vediamo che i risultati sono molto vicini a quelli ottenuti con l’approccio Monte Carlo, con i pesi che si trovano all’interno di un paio di punti percentuali l’uno dall’altro.
Codice completo
In questo articolo abbiamo descritto come ottimizzare l’asset allocation di un portafoglio di investimenti con Python. Per il codice completo riportato in questo articolo, si può consultare il seguente repository di github:
https://github.com/datatrading-info/Asset_Management