In questo articolo esaminiamo l’ottimizzazione di un portafoglio di investimenti con Python, includendo il fondamentale concetto di diversificazione e la creazione di una frontiera efficiente. Concetti usati dagli investitori per scegliere specifici mix di asset in base agli obiettivi di investimento. In altre parole un compromesso tra il livello desiderato di rendimento del portafoglio e il livello desiderato di rischio del portafoglio.
Teora del portafoglio
Investopedia definisce la “Teoria del portafoglio” come: “La Modern Portfolio Theory (MPT), un’ipotesi avanzata da Harry Markowitz nel suo articolo “Portfolio Selection” (pubblicato nel 1952 dal Journal of Finance) è una teoria di investimento basata sull’idea che gli investitori avversi al rischio possono costruire portafogli per ottimizzare o massimizzare il rendimento atteso sulla base di un determinato livello di rischio di mercato, sottolineando che il rischio è parte integrante di una ricompensa più elevata. È una delle teorie economiche più importanti e influenti in ambito delle finanza e degli investimenti.
Chiamata anche “teoria del portafoglio” o “teoria della gestione del portafoglio”, la MPT suggerisce la possibilità di costruire una “frontiera efficiente” di portafogli ottimali, cioè i portafogli che offrono il massimo rendimento possibile per un dato livello di rischio. Suggerisce che non è sufficiente esaminare il rischio e il rendimento attesi di un particolare titolo. Investendo in più di un titolo, un investitore può raccogliere i vantaggi della diversificazione, in particolare una riduzione del rischio complessivo del portafoglio. La MPT quantifica i vantaggi della diversificazione, cioè i vantaggi di non mettere tutte le uova nello stesso paniere.
È molto semplice eseguire alcune righe di Python per scaricare i dati per un singolo titolo, calcolare il rendimento giornaliero medio e la deviazione standard dei rendimenti. Questi dati sono quindi annualizzati per ottenere il rendimento annuo medio previsto e la volatilità di quel singolo titolo. Nel seguente esempio scegliamo il titolo Apple.
import yfinance as yf
import numpy as np
import pandas as pd
stock = ['AAPL']
data = yf.download(stock,start='2010-01-01', end='2020-01-01')['Adj Close']
data.sort_index(inplace=True)
returns = data.pct_change()
mean_return = returns.mean()
return_stdev = returns.std()
annualised_return = round(mean_return * 252,2)
annualised_stdev = round(return_stdev * np.sqrt(252),2)
print(f'The annualised mean return of stock {stock[0]} is {annualised_return}, and the annualised volatility is {annualised_stdev}')
Otteniamo i seguenti valori:
The annualised mean return of stock AAPL is 0.27, and the annualised volatility is 0.26
Ovviamente questi semplici calcoli possono essere eseguiti per qualsiasi titolo, ma la maggior parte dei portafogli degli investitori sono formati da molti titoli, fino a decine di titoli e a volte centinaia di titoli. Dobbiamo sottolineare una regola dei portafoglio: il vantaggio marginale della diversificazione si riduce all’aumentare del numero di titoli. In altre parole, il vantaggio di diversificazione che si ottiene passando da 1 titolo a 2 titoli, è maggiore di quando si passa da 2 titoli a 3 titoli e così via. Questa è solo una regola generale e gli effettivi vantaggi di diversificazione di un determinato titolo dipendono dalla sua correlazione con il portafoglio esistente.
Da quanto sopra possiamo dedurre che non dobbiamo interessarci al rendimento atteso e la volatilità (deviazione standard) dei singoli titoli, ma dobbiamo concentrarci sulle informazioni relative al portafoglio di titoli nel suo complesso. In questo modo catturiamo i vantaggi della diversificazione di un portafoglio costituiti da asset non correlati.
Simulazione dei pesi degli asset
Supponiamo ora di avere un portafoglio costituito da 4 titoli tecnologici, Apple, Microsoft, Amazon e Facebook. Il nostro obiettivo è calcolare il rendimento atteso e la volatilità del portafoglio. Abbiamo bisogno di definire i pesi dei singoli titoli all’interno del portafoglio, ovvero la quantità di ogni titolo come percentuale delle partecipazioni dell’intero portafoglio. Ad esempio consideriamo un portafoglio composto per il 50% da azioni Apple, per il 20% da azioni Microsoft, per il 20% da azioni Amazon e per il 10% da Facebook. Possiamo calcolare il rendimento atteso e la volatilità del portafoglio come segue:
# lista titoli in portafoglio
# ATTENZIONE CHE QUESTI DEVONO ESSERE INSERITI IN ORDINE ALFABETICO PER I RISULTATI CORRETTI!!!
stocks = ['AAPL','AMZN','MSFT','FB']
# download dei dati dei prezzi giornalieri per ogni azione nel portafoglio
data = yf.download(stocks, start='2010-01-01', end='2020-01-01')['Adj Close']
data.sort_index(inplace=True)
# converte i prezzi giornalieri in rendimenti giornalieri
returns = data.pct_change()
# calcolo della media e la covarianza dei redimenti giornalieri
mean_daily_returns = returns.mean()
cov_matrix = returns.cov()
# Definizione dei pesi del portafoglio
weights = np.asarray([0.5,0.2,0.2,0.1])
# calcolo del rendimento annualizzato del portafoglio
portfolio_return = round(np.sum(mean_daily_returns * weights) * 252,2)
# calcolo della volatilità annualizzata del portafoglio
portfolio_std_dev = round(np.sqrt(np.dot(weights.T,np.dot(cov_matrix, weights))) * np.sqrt(252),2)
print(f'Portfolio expected annualised return is {portfolio_return} and volatility is {portfolio_std_dev}')
Otteniamo i seguenti valori
Portfolio expected annualised return is 0.28 and volatility is 0.21
Abbiamo ottenuto il rendimento atteso e la volatilità dell’attuale portafoglio. Cosa succede se non siamo soddisfatti del livello di volatilità dell’attuale portafoglio e vogliamo ridurlo? E se vogliamo assumerci più rischi per ottenere un rendimento atteso più elevato? Come possiamo riorganizzare i peso di ciascun titolo nel portafoglio per raggiungere questi obiettivi?
Possiamo iniziare modificando manualmente i valori nell’array dei pesi nel codice precedente, eseguire nuovamente lo script e vediamo i valori del rendimento atteso e della volatilità ottenuti per quel particolare insieme di pesi. Questo è un approccio MOLTO manuale. Ci sono teoricamente un numero infinito di serie di pesi di portafoglio da testare, quindi non è un approccio pratico.
Fortunatamente possiamo usare la simulazione Monte Carlo per eseguire migliaia di test con pesi diversi, generati casualmente per i singoli titoli (ovviamente assicurandoci che la somma dei pesi sia pari al 100%). Dobbiamo quindi calcolare il rendimento atteso, la volatilità attesa e lo Sharpe ratio per ciascuno dei titoli nei portafogli generati casualmente.
Inoltre è molto semplice (e utile) tracciare tutte le combinazioni dei rendimenti attesi e delle volatilità su un grafico a dispersione. Possiamo persino colorare i dati in base allo Sharpe Ratio di quel particolare portafoglio.
import numpy as np
import pandas as pd
import yfinance as yf
import matplotlib.pyplot as plt
# Lista dei titoli in portafoglio
stocks = ['AAPL', 'AMZN', 'MSFT', 'FB']
# Download dei dati dei prezzi giornalieri per ogni azione nel portafoglio
data = yf.download(stocks, start='2010-01-01', end='2020-01-01')['Adj Close']
data.sort_index(inplace=True)
# Converte i prezzi giornalieri in rendimenti giornalieri
returns = data.pct_change()
# Calcolo della media e la covarianza dei redimenti giornalieri
mean_daily_returns = returns.mean()
cov_matrix = returns.cov()
# Imposta il numero di simulazioni
num_portfolios = 25000
# Imposta un array dei risultati
results = np.zeros((3, num_portfolios))
for i in range(num_portfolios):
# Selezioni di pesi random
weights = np.random.random(4)
# Ribilanciamento dei pesi per avere somma 1
weights /= np.sum(weights)
# Calcolo dei rendimenti e volatilità del portafoglio
portfolio_return = np.sum(mean_daily_returns * weights) * 252
portfolio_std_dev = np.sqrt(np.dot(weights.T, np.dot(cov_matrix, weights))) * np.sqrt(252)
# Memorizzazioni nell'array dei risultati
results[0, i] = portfolio_return
results[1, i] = portfolio_std_dev
# Memorizzazione dello Sharpe Ratio - elemento risk free escluso per semplicità
results[2, i] = results[0, i] / results[1, i]
# Converi l'array dei risultati in un dataframe pandas
results_frame = pd.DataFrame(results.T, columns=['ret', 'stdev', 'sharpe'])
# Crea un grafico scatter colorato dallo Sharpe Ratio
plt.scatter(results_frame.stdev, results_frame.ret, c=results_frame.sharpe, cmap='RdYlBu')
plt.colorbar()
plt.show()
print("")
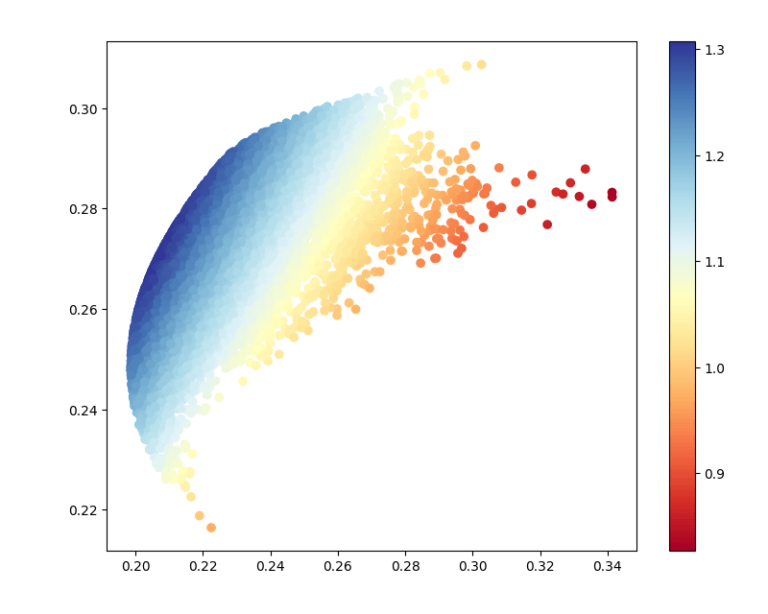
Nel grafico vediamo come la modifica del peso di ciascun titolo nel portafoglio può avere un effetto drammatico sul rendimento atteso e sul livello di rischio (deviazione standard/volatilità) a cui è esposto l’investitore.
Ad esempio, un rendimento del 18% può essere ottenuto tramite portafogli con una volatilità di poco inferiore al 20%, ma anche tramite portafogli che condividono lo stesso rendimento atteso con una volatilità pari a poco più del 28%. Dobbiamo quindi prestare molta attenzione alla definizione del peso che ciascuno titolo dovrebbe avere nel portafoglio.
Portafogli efficienti
Possiamo evidenziare due portafogli “speciali”:
- il portafoglio con il più alto Sharpe Ratio (cioè i rendimenti più alti corretti per il rischio)
- Il “portafoglio a varianza minima”, cioè è il portafoglio con la volatilità più bassa.
Possiamo individuare questi 2 portafogli modificando il codice per memorizzare tutte le combinazioni di pesi casuali, usati per ogni simulazione Monte Carlo, insieme al rendimento atteso, alla deviazione standard e al Sharpe Ratio. Individuiamo quindi i valori nel dataframe dei risultati dove lo Sharpe Ratio è più alto per il portafoglio “1” e dove la deviazione standard è più bassa per il portafoglio “2”. Infine possiamo estrarre i pesi che corrispondono ai due portafoglio, dato che li abbiamo memorizzati in un array durante l’elaborazione delle simulazioni.
import numpy as np
import pandas as pd
import yfinance as yf
import matplotlib.pyplot as plt
# Lista dei titoli in portafoglio
stocks = ['AAPL', 'AMZN', 'MSFT', 'FB']
# Download dei dati dei prezzi giornalieri per ogni azione nel portafoglio
data = yf.download(stocks, start='2010-01-01', end='2020-01-01')['Adj Close']
data.sort_index(inplace=True)
# Converte i prezzi giornalieri in rendimenti giornalieri
returns = data.pct_change()
# Calcolo della media e la covarianza dei redimenti giornalieri
mean_daily_returns = returns.mean()
cov_matrix = returns.cov()
# Imposta il numero di simulazioni
num_portfolios = 25000
# Imposta un array dei risultati
results = np.zeros((7, num_portfolios))
for i in range(num_portfolios):
# Selezioni di pesi random
weights = np.array(np.random.random(4))
# Ribilanciamento dei pesi per avere somma 1
weights /= np.sum(weights)
# Calcolo dei rendimenti e volatilità del portafoglio
portfolio_return = np.sum(mean_daily_returns * weights) * 252
portfolio_std_dev = np.sqrt(np.dot(weights.T, np.dot(cov_matrix, weights))) * np.sqrt(252)
# Memorizzazioni nell'array dei risultati
results[0, i] = portfolio_return
results[1, i] = portfolio_std_dev
# Memorizzazione dello Sharpe Ratio - elemento risk free escluso per semplicità
results[2, i] = results[0, i] / results[1, i]
# ciclo sul vettore dei pesi e aggiunta dei dati sull'array dei risultati
for j in range(len(weights)):
results[j + 3, i] = weights[j]
# Converte l'array dei risultati in un dataframe pandas
results_frame = pd.DataFrame(results.T, columns=['ret', 'stdev', 'sharpe', stocks[0], stocks[1], stocks[2], stocks[3]])
# Individua il portafoglio con il Sharpe Ratio maggiore
max_sharpe_port = results_frame.iloc[results_frame['sharpe'].idxmax()]
# Individua il portafoglio con la deviazione standard minima
min_vol_port = results_frame.iloc[results_frame['stdev'].idxmin()]
# Crea il grafico scatter colorato dallo Sharpe Ratio
plt.scatter(results_frame.stdev, results_frame.ret, c=results_frame.sharpe, cmap='RdYlBu')
plt.xlabel('Volatility')
plt.ylabel('Returns')
plt.colorbar()
# Visualizza una stella rossa per evidenziare il portafoglio con lo Sharpe Ratio maggiore
plt.scatter(max_sharpe_port[1], max_sharpe_port[0], marker=(5, 1, 0), color='r', s=1000)
# Visualizza una stella verde per evidenziare il portafoglio con la varianza minima
plt.scatter(min_vol_port[1], min_vol_port[0], marker=(5, 1, 0), color='g', s=1000)
plt.show()
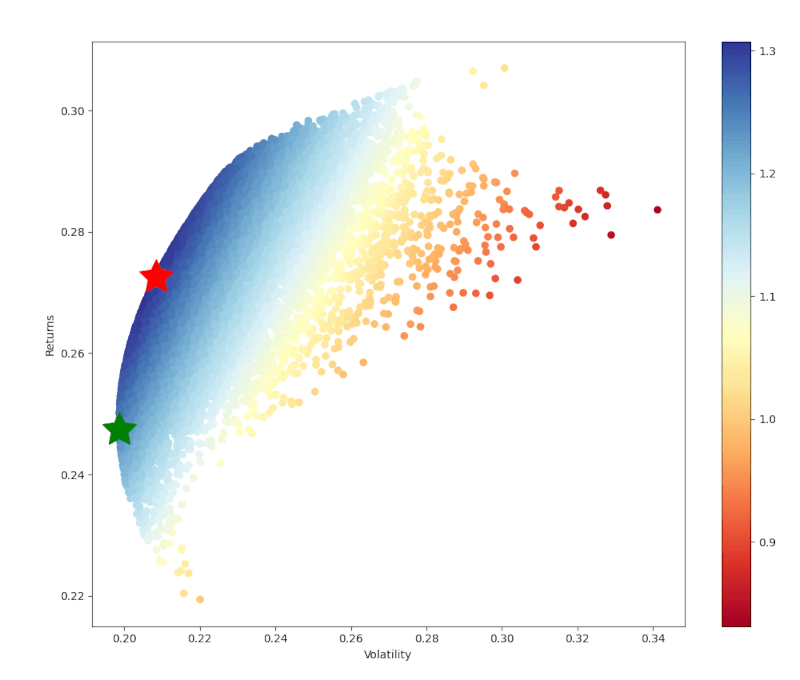
Non resta che estrarre i pesi dei titoli necessari per creare i due portafogli sopra evidenziati con il seguente comando:
print(max_sharpe_port)
ret 0.272389
stdev 0.208348
sharpe 1.307378
AAPL 0.401140
AMZN 0.248156
MSFT 0.146871
FB 0.203833
print(min_vol_port)
ret 0.248423
stdev 0.198650
sharpe 1.250556
AAPL 0.326294
AMZN 0.070578
MSFT 0.118966
FB 0.484162
Codice completo
In questo articolo abbiamo descritto l’ottimizzazione di un portafoglio di investimenti con Python. Per il codice completo riportato in questo articolo, si può consultare il seguente repository di github:
https://github.com/datatrading-info/Asset_Management