Negli articoli precedenti abbiamo introdotto le basi matematiche dei modelli spaziali statali e dei filtri di Kalman, nonché l’applicazione della libreria pykalman a una coppia di ETF per regolare dinamicamente un rapporto di copertura come base per una strategia di trading mean-reverting.
In questo articolo descriviamo una strategia di trading originariamente introdotta da Ernest Chan (2012) [1] e testata da Aidan O’Mahony su Quantopian [2]. Usiamo il nostro framework di backtesting open source DataTrader, basato su Python, per implementare la strategia. DataTrader si occuperà del “lavoro sporco” per il tracciamento della posizione, la gestione del portafoglio e dell’acquisizione dei dati, mentre ci concentreremo esclusivamente sul codice che genera i segnali di trading.
La strategia di trading
Applichiamo la strategia di pairs-trading a una coppia di Exchange Traded Funds (ETF) che replicano entrambi la performance delle obbligazioni del Tesoro USA di durata variabile. Sono:
L’obiettivo è costruire una strategia di ritorno alla media con questa coppia di ETF.
In realtà, lo “spread” sintetico tra TLT e IEI è la serie storica dove ci interessa operare, andare long o short. Il filtro di Kalman viene utilizzato per tracciare dinamicamente il rapporto di copertura tra i due strumenti in modo da mantenere stazionario lo spread (e quindi il ritorno alla media).
Per creare le regole di trading è necessario determinare quando lo spread si è allontano troppo dal suo valore atteso. Come determiniamo quando è “troppo lontano”? Potremmo utilizzare un insieme di valori assoluti fissi, ma questi dovrebbero essere determinati empiricamente. Ciò introdurrebbe nel sistema un ulteriore parametro variabile che richiederebbe un’ottimizzazione (e quindi un pericolo di overfitting).
Un approccio “senza parametri” per creare questi valori consiste nel considerare multipli della deviazione standard dello spread e utilizzarli come limiti. Per semplicità possiamo impostare il coefficiente di molteplicità uguale a uno.
Quindi possiamo “andare long sullo spread” se l’errore di previsione scende al di sotto della deviazione standard negativa dello spread. Rispettivamente possiamo “andare short sullo spread” se l’errore di previsione supera la deviazione standard positiva dello spread. Le regole di uscita sono semplicemente l’opposto delle regole di ingresso.
Il rapporto di copertura dinamico è rappresentato da un componente del vettore degli stati nascosti al tempo t, \(\theta_t\), che indicheremo come \(\theta^0_t\). Questo è il valore della pendenza “beta”, ben nota nella regressione lineare.
“Andare long sullo spread” significa acquistare (long) N unità di TLT e vendere (short) \(\lfloor{ \theta^0_t N \rfloor}\) unità di IEI, dove \(\lfloor{ x \rfloor}\) è il “piano” che rappresenta il primo intero minore di x. Quest’ultimo è necessario dato che dobbiamo negoziare un numero intero di quote degli ETF. “Andare short lo spread” è l’opposto del long, N definisce la dimensione complessiva della posizione.
\(e_t\) rappresenta l’errore di forecast o l’errore residuo della previsione al tempo t, mentre \(Q_t\) rappresenta la varianza di questa previsione al tempo t.
In dettaglio, la strategia prevede le seguenti regole:
- \(e_t \lt -\sqrt{Q_t}\) – Entrata Long: andare long con N azioni di TLT e andare short con \(\lfloor{ \theta^0_t N \rfloor}\) azioni di IEI
- \(e_t \ge -\sqrt{Q_t}\) – Uscita long: chiudere tutte le posizioni long di TLT e IEI
- \(e_t \gt \sqrt{Q_t}\) – Entrata Short: andare short con N azioni di TLT e andare long con \(\lfloor{ \theta^0_t N \rfloor}\) azioni di IEI
- \(e_t \le \sqrt{Q_t}\) – Uscita Short: chiudere tutte le posizioni short di TLT e IEI
Il ruolo del filtro di Kalman è quello di aiutarci a calcolare \(\theta_t\), così come \(e_t\) e \(Q_t\). \(\theta_t\) rappresenta il vettore dei valori della pendenza e dell’intercetta della regressione lineare tra TLT e IEI al tempo t, che sono stimati dal filtro di Kalman. L’errore/residuo di previsione \(e_t = y_t – \hat{y}_t\) è la differenza tra il valore effettivo di TLT oggi e la stima del filtro di Kalman di TLT oggi. \(Q_t\) è la varianza delle previsioni, di conseguenza \(\sqrt{Q_t}\) corrisponde alla deviazione standard della previsione.
Per maggiori dettagli sulle modalità di calcolo di questi parametri si rimanda all’articolo sul modello dello spazio degli stati e il filtro di Kalman.
La strategia prevede un processo composto dalle seguenti fasi:
- Acquisizione delle barre OHLCV giornaliere per TLT e IEI.
- Uso ricorsivo del filtro di Kalman per stimare il prezzo di TLT di oggi sulla base delle osservazioni di ieri di IEI
- Calcolo della differenza tra la stima di Kalman di TLT e il valore effettivo, spesso chiamato errore di previsione o errore residuo , che è una misura di quanto lo spread di TLT e IEI si allontana dal suo valore atteso
- Andare long quando il movimento è molto inferiore dal valore atteso e corrispondentemente andare short quando il movimento è molto superiore al valore atteso
- Uscire dalle posizioni long e short quando la serie torna al valore atteso
Dati
Per attuare questa strategia è necessario disporre di dati OHLCV sui prezzi per il periodo coperto da questo backtest. In particolare è necessario scaricare quanto segue:
- TLT – Per il periodo dal 3 agosto 2009 al 1 agosto 2016 (link qui )
- IEI Per il periodo dal 3 agosto 2009 al 1 agosto 2016 (link qui ).
se si desidera replicare i risultati questi dati dovranno essere inseriti nella directory specificata dal file di configurazione di DataTrader,
Implementazione Python con DataTrader
Poiché DataTrader gestisce il tracciamento della posizione, la gestione del portafoglio, l’acquisizione dei dati e la gestione degli ordini, l’unico codice che dobbiamo scrivere riguarda la classe Strategy.
La classe Strategy comunica con il PortfolioHandler tramite la coda degli eventi, utilizzando gli oggetti SignalEvent. Inoltre dobbiamo importare la classe della strategia astratta di base, AbstractStrategy.
Da notare che nell’attuale versione di DataTrader dobbiamo importare la classe PriceParser. Questa classe fornisce le funzioni per moltiplicare tutti i prezzi in ingresso per un multiplo elevato (\(10^8\)) ed eseguire operazioni aritmetiche con numeri interi durante il rilevamento delle posizioni. In questo modo evitiamo problemi di arrotondamento in virgola mobile che possono accumularsi in backtest su periodi molto lunghi. Dobbiamo dividere tutti i risultati per PriceParser.PRICE_MULTIPLIER in modo da ottenere i valori corretti:
from math import floor
import numpy as np
from datatrader.price_parser import PriceParser
from datatrader.event import (SignalEvent, EventType)
from datatrader.strategy.base import AbstractStrategy
Il passaggio successivo è creare la classe KalmanPairsTradingStrategy. Il compito di questa classe è determinare quando creare oggetti SignalEvent in base ai messaggi ricevuti dai dati di mercato BarEvent, cioè barre OHLCV giornaliere di TLT e IEI da Yahoo Finance.
Ci sono molti modi diversi per organizzare questa classe. Per facilitare la descrizione del codice, abbiamo codificato tutti i parametri della classe. In particolare abbiamo corretto il valore di \(\delta=10^{-4}\) e di \(v_t=10^{-3}\). Questi rappresentano il rumore del sistema e la varianza del rumore delle misurazioni nel modello del filtro di Kalman. Questi potrebbero anche essere implementati come argomenti di una parola chiave nel costruttore __init__ della classe. Un tale approccio consentirebbe una semplice ottimizzazione dei parametri.
Il primo compito è impostare i parametri time e invested in modo che siano uguali a None, poiché verranno aggiornati man mano che i dati di mercato vengono accettati e vengono generati segnali di trading. latest_prices è una doppia matrice che contiene gli ultimi prezzi di TLT e IEI, utilizzata per comodità all’interno della classe.
Il successivo set di parametri si riferiscono al filtro di Kalman e sono spiegati in modo approfondito nei due articoli precedenti qui e qui .
Il set finale di parametri include days, utilizzato per tracciare quanti giorni sono trascorsi, nonché qty e cur_hedge_qty, utilizzato per tracciare le quantità assolute di ETF da acquistare sia per il lato long che per quello short. In questo caso abbiamo impostato 2.000 unità su un patrimonio netto di 100.000 USD.
class KalmanPairsTradingStrategy(AbstractStrategy):
"""
Requisiti:
tickers - Lista dei simboli dei ticker
events_queue - Manager del sistema della coda degli eventi
short_window - numero di barre per la moving average di breve periodo
long_window - numero di barre per la moving average di lungo periodo
"""
def __init__(
self, tickers, events_queue
):
self.tickers = tickers
self.events_queue = events_queue
self.time = None
self.latest_prices = np.array([-1.0, -1.0])
self.invested = None
self.delta = 1e-4
self.wt = self.delta / (1 - self.delta) * np.eye(2)
self.vt = 1e-3
self.theta = np.zeros(2)
self.P = np.zeros((2, 2))
self.R = None
self.C = None
self.days = 0
self.qty = 2000
self.cur_hedge_qty = self.qty
Il metodo successivo _set_correct_time_and_price è un metodo “di appoggio” utilizzato per garantire che il filtro Kalman abbia tutte le corrette informazioni sui prezzi disponibili al momento giusto. Ciò è necessario perché in un sistema di backtest basato su eventi come DataTrader le informazioni sul mercato arrivano in sequenza.
Potremmo trovarci nello scenario dove in giornata K abbiamo ricevuto un prezzo per IEI, ma non TFT. Quindi dobbiamo aspettare fino a che entrambi gli eventi Market di TFT e IEI siano entranti nel ciclo di backtest, attraverso la coda degli eventi. Nel trading dal vivo questo non è un problema poiché questi eventi arriveranno quasi rispetto al periodo di trading di pochi giorni. Tuttavia, in un backtest basato sugli eventi, dobbiamo attendere l’arrivo di entrambi i prezzi prima di aggiornare i valori del filtro di Kalman.
Il codice controlla essenzialmente se l’evento successivo è relativo al giorno corrente. In tal caso, il prezzo corretto viene aggiunto all’elenco latest_price di TLT e IEI. Se abbiamo un nuovo giorno, si ripristina l’elenco latest_price e i prezzi corretti sono di nuovo aggiunti.
In futuro questo tipo di metodo di “pulizia” sarà probabilmente inserito nel codice base di DataTrader, riducendo la necessità di scrivere codice “boilerplate”, ma per ora dobbiamo prevederlo all’interno della nostra strategia.
def _set_correct_time_and_price(self, event):
"""
Impostazione del corretto prezzo e timestamp dell'evento
estratto in ordine dalla coda degli eventi.
"""
# Impostazione della prima istanza di time
if self.time is None:
self.time = event.time
# Correzione degli ultimi prezzi, che dipendono dall'ordine in cui
# arrivano gli eventi delle barre di mercato
price = event.adj_close_price/PriceParser.PRICE_MULTIPLIER
if event.time == self.time:
if event.ticker == self.tickers[0]:
self.latest_prices[0] = price
else:
self.latest_prices[1] = price
else:
self.time = event.time
self.days += 1
self.latest_prices = np.array([-1.0, -1.0])
if event.ticker == self.tickers[0]:
self.latest_prices[0] = price
else:
self.latest_prices[1] = price
Il nucleo della strategia risiede nel metodo calculate_signals. Per prima cosa impostiamo i tempi e i prezzi corretti (come descritto in precedenza). Quindi controlliamo di avere entrambi i prezzi di TLT e IEI, a quel punto possiamo considerare nuovi segnali di trading.
y è impostato pari all’ultimo prezzo di IEI, mentre F è la matrice di osservazione contenente l’ultimo prezzo di TLT, nonché come variabile unitaria per rappresentare l’intercetta della regressione lineare. Il filtro di Kalman viene successivamente aggiornato con questi ultimi prezzi. Infine calcoliamo l’errore di previsione \(e_t\) e la deviazione standard delle previsioni, \(\sqrt{Q_t}\). Esaminiamo questo codice passo dopo passo, poiché sembra un po’ complicato.
Il primo compito è calcolare il valore scalare y e la matrice di osservazione F, che contengono rispettivamente i prezzi di IEI e e TLT. Calcoliamo la matrice varianza-covarianza R o la impostiamo come una matrice di zeri nel caso non sia stata ancora inizializzata. Successivamente calcoliamo la nuova previsione per l’osservazione yhat così come l’errore di previsione et.
Calcoliamo quindi la varianza delle previsioni di osservazione Qt e la deviazione standard sqrt_Qt. Usiamo le regole di aggiornamento descritte dal modello dello spazio degli stati per ottenere la distribuzione a posteriori degli stati theta, che contiene il rapporto di copertura / pendenza tra i due prezzi:
def calculate_signals(self, event):
"""
Calculo dei segnali della stategia con il filtro di Kalman.
"""
if event.type == EventType.BAR:
self._set_correct_time_and_price(event)
# Opera solo se abbiamo entrambe le osservazioni
if all(self.latest_prices > -1.0):
# Creare la matrice di osservazione degli ultimi prezzi di
# TLT e il valore dell'intercetta nonché il
# valore scalare dell'ultimo prezzo di IEI
F = np.asarray([self.latest_prices[0], 1.0]).reshape((1, 2))
y = self.latest_prices[1]
# Il valore a priori degli stati \theta_t è una distribuzione
# gaussiana multivariata con media a_t e varianza-covarianza R_t
if self.R is not None:
self.R = self.C + self.wt
else:
self.R = np.zeros((2, 2))
# Calcola l'aggiornamento del filtro di Kalman
# ----------------------------------
# Calcola la previsione di una nuova osservazione
# e il relativo errore di previsione
yhat = F.dot(self.theta)
et = y - yhat
# Q_t è la varianza della previsione delle osservazioni
# e sqrt{Q_t} è la deviazione standard delle previsioni
Qt = F.dot(self.R).dot(F.T) + self.vt
sqrt_Qt = np.sqrt(Qt)
# Il valore a posteriori degli stati \theta_t ha una
# distribuzione gaussiana multivariata con
# media m_t e varianza-covarianza C_t
At = self.R.dot(F.T) / Qt
self.theta = self.theta + At.flatten() * et
self.C = self.R - At * F.dot(self.R)
cur_hedge_qty quando andiamo long o short come come la pendenza \(\theta^0_t\) si adegua costantemente nel tempo:
# Opera solo se i giorni sono maggiori del
# periodo di "riscaldamento"
if self.days > 1:
# Se non siamo a mercato...
if self.invested is None:
if et < -sqrt_Qt:
# Entrata Long
print("LONG: %s" % event.time)
self.cur_hedge_qty = int(floor(self.qty*self.theta[0]))
self.events_queue.put(SignalEvent(self.tickers[1], "BOT", self.qty))
self.events_queue.put(SignalEvent(self.tickers[0], "SLD", self.cur_hedge_qty))
self.invested = "long"
elif et > sqrt_Qt:
# Entrata Short
print("SHORT: %s" % event.time)
self.cur_hedge_qty = int(floor(self.qty*self.theta[0]))
self.events_queue.put(SignalEvent(self.tickers[1], "SLD", self.qty))
self.events_queue.put(SignalEvent(self.tickers[0], "BOT", self.cur_hedge_qty))
self.invested = "short"
# Se siamo a mercato...
if self.invested is not None:
if self.invested == "long" and et > -sqrt_Qt:
print("CLOSING LONG: %s" % event.time)
self.events_queue.put(SignalEvent(self.tickers[1], "SLD", self.qty))
self.events_queue.put(SignalEvent(self.tickers[0], "BOT", self.cur_hedge_qty))
self.invested = None
elif self.invested == "short" and et < sqrt_Qt:
print("CLOSING SHORT: %s" % event.time)
self.events_queue.put(SignalEvent(self.tickers[1], "BOT", self.qty))
self.events_queue.put(SignalEvent(self.tickers[0], "SLD", self.cur_hedge_qty))
self.invested = None
Questo è tutto il codice necessario per l’oggetto Strategy. Abbiamo anche bisogno di creare un file di backtest per incapsulare tutta la nostra logica di trading e la scelta delle classi da usare. Questa specifica versione è molto simile a quelle presenti nella directory examples e sostituisce il capitale di 500.000 USD con 100.000 USD.
Si sostituisce inoltre il FixedPositionSizer con il NaivePositionSizer. Quest’ultimo viene utilizzato per accettare “ingenuamente” le quantità assolute di quote ETF da negoziare così come suggerite nella classe KalmanPairsTradingStrategy. In un ambiente reale sarebbe necessario adeguarlo a seconda degli obiettivi di gestione del rischio del portafoglio.
Ecco il codice completo per kalman_datatrader_backtest.py:
import datetime
from datatrader import settings
from datatrader.compat import queue
from datatrader.price_parser import PriceParser
from datatrader.price_handler.yahoo_daily_csv_bar import YahooDailyCsvBarPriceHandler
from datatrader.strategy.base import Strategies # DisplayStrategy
from datatrader.position_sizer.naive import NaivePositionSizer
from datatrader.risk_manager.example import ExampleRiskManager
from datatrader.portfolio_handler import PortfolioHandler
from datatrader.compliance.example import ExampleCompliance
from datatrader.execution_handler.ib_simulated import IBSimulatedExecutionHandler
from datatrader.statistics.tearsheet import TearsheetStatistics
from datatrader.trading_session import TradingSession
from kalman_datatrader_strategy import KalmanPairsTradingStrategy
def run(config, testing, tickers, filename):
# Impostazione delle variabili necessarie per il backtest
# Informazioni sul Backtest
title = ['Kalman Filter Example on TLT and IEI: 100x300']
initial_equity = 100000.00
start_date = datetime.datetime(2009, 8, 1)
end_date = datetime.datetime(2016, 8, 1)
events_queue = queue.Queue()
# Uso del Manager dei Prezzi di Yahoo Daily
price_handler = YahooDailyCsvBarPriceHandler(config.CSV_DATA_DIR, events_queue,
tickers, start_date=start_date, end_date=end_date)
# Uso della strategia KalmanPairsTrading
strategy = KalmanPairsTradingStrategy(tickers, events_queue)
strategy = Strategies(strategy)
# Uso di un Position Sizer standard
position_sizer = NaivePositionSizer()
# Uso di Manager di Risk di esempio
risk_manager = ExampleRiskManager()
# Use del Manager di Portfolio di default
portfolio_handler = PortfolioHandler(
PriceParser.parse(initial_equity), events_queue, price_handler,
position_sizer, risk_manager
)
# Uso del componente ExampleCompliance
compliance = ExampleCompliance(config)
# Uso un Manager di Esecuzione che simula IB
execution_handler = IBSimulatedExecutionHandler(
events_queue, price_handler, compliance
)
# Uso delle statistiche di default
statistics = TearsheetStatistics(
config, portfolio_handler, title=""
)
# Settaggio del backtest
backtest = TradingSession(
config, strategy, tickers,
initial_equity, start_date, end_date, events_queue,
price_handler=price_handler,
portfolio_handler=portfolio_handler,
compliance=compliance,
position_sizer=position_sizer,
execution_handler=execution_handler,
risk_manager=risk_manager,
statistics=statistics,
sentiment_handler=None,
title=title, benchmark=None
)
results = backtest.start_trading(testing=testing)
statistics.save(filename)
return results
def main(config, testing, tickers, filename):
tickers = tickers.split(",")
config = settings.from_file(config, testing)
run(config, testing, tickers, filename)
if __name__ == "__main__":
config = './datatrader.yml'
testing = False
tickers = 'TLT,IEI'
filename = None
main(config, testing, tickers, filename)
Se DataTrader è installato correttamente e i dati sono stati scaricati da Yahoo Finance, il codice può essere eseguito tramite il seguente comando da terminale:
$ python kalman_datatrader_backtest.py
Grazie ad alcuni miglioramenti, il codice è ottimizzato per lavorare con dati rapresentati come barre OHLCV ed esegue il backtesting in tempi più rapidi.
Risultati della strategia
Una delle funzionalità implementate in DataTrader è quella del “tearsheet” che permette la produzione di un report che raccoglie le statistiche e le performance della strategia.
Il tearsheet è usato principalmente come report “one pager” di una strategia di trading. La classe TearsheetStatistics nella base di codice DataTrader replica molte delle statistiche presenti in un tipico report sulle prestazioni della strategia.
I primi due grafici rappresentano rispettivamente la curva equity e la percentuale di drawdown. Sotto questo ci sono i pannelli delle prestazioni mensili e annuali. Infine vengono presentate la curva del patrimonio netto, le statistiche a livello di trade e temporali:
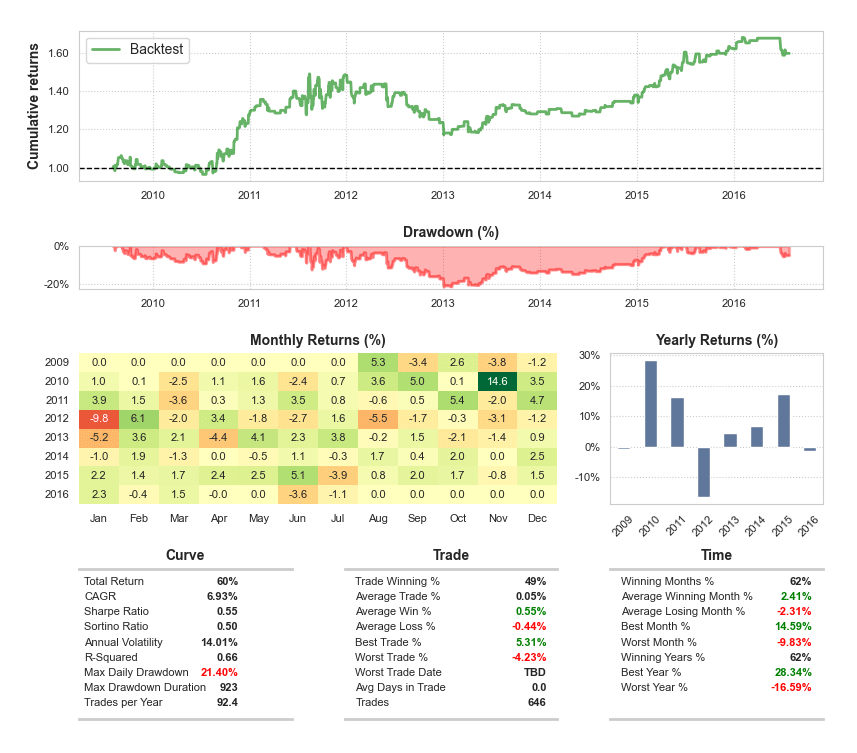
La curva di equity inizia relativamente piatta per il primo anno della strategia, ma si intensifica rapidamente durante il 2011. Durante il 2012 la strategia diventa significativamente più volatile rimanendo “sott’acqua” fino al 2015 e raggiungendo una percentuale massima di drawdown del 15,79%. La performance aumenta gradualmente dal drawdown alla fine del 2013 fino al 2016.
La strategia ha un CAGR dell’6,93% con uno Sharpe Ratio di 0,55. Ha anche una durata massima di drawdown di 923 giorni – quasi tre anni! Si noti che questa strategia viene eseguita al lordo dei costi di transazione, quindi la performance reale sarebbe probabilmente peggiore.
Prossimi passi
E’ necessario molto lavoro di ricerca per trasformare questo in una strategia redditizia da implementare in un trading dal vivo. Le potenziali aree di miglioramenti includono:
- Ottimizzazione dei parametri – Variazione dei parametri del filtro Kalman tramite la ricerca nella griglia di convalida incrociata o una qualche forma di ottimizzazione di apprendimento automatico. Tuttavia, questo introduce la netta possibilità di overfitting ai dati storici.
- Selezione degli asset – La scelta di coppie di ETF aggiuntive o alternative aiuterebbe ad aggiungere diversificazione al portafoglio, ma aumenta la complessità della strategia così come il numero di operazioni (e quindi i costi di transazione).
Nei prossimi articoli considereremo come eseguire queste procedure per varie strategie di trading.
Riferimenti
- [1] Chan, E. P. (2013) Algorithmic Trading: Winning Strategies and their Rationale, Wiley
- [2] O’Mahony, A. (2014) Ernie Chan’s EWA/EWC pair trade with Kalman filter, https://www.quantopian.com/posts/ernie-chans-ewa-slash-ewc-pair-trade-with-kalman-filter
Codice completo
Per il codice completo riportato in questo articolo, utilizzando il framework open-source di backtesting event-driven DataTrader si può consultare il seguente repository di github:
https://github.com/datatrading-info/DataTrader