In questo articolo descriviamo un approccio al trading con il reinforcement learning in Python per creare un modello di machine learning per determinare quali operazioni eseguire.
Nel precedente articolo abbiamo descritto il gradient ascent e come possiamo usarlo per massimizzare una funzione di ricompensa. In questo articolo, invece di usare l’errore quadratico medio come funzione di ricompensa, usiamo lo Sharpe Ratio. Possiamo usare il reinforcement learning per massimizzare lo Sharpe Ratio su un data set di addestramento e provare a creare una strategia con un elevato Sharpe Ratio quando è testata su dataset fuori dal campione.
Lo Sharpe Ratio
Lo Sharpe Ratio è un indicatore molto usato per misurare la performance di un investimento nel tempo corretta per il rischio. Supponendo un tasso privo di rischio pari a 0, la formula per calcolare lo Sharpe Ratio è semplicemente il rendimento medio dell’investimento diviso per la deviazione standard dei rendimenti, come segue:
\(S_T = {A \over \sqrt{B – A^2}}\)
dove \(A={1\over T}\sum\limits _{t=1}^{T}R _t\) e \(B={1\over T}\sum\limits _{t=1}^{T}R _t^2\)
Lo Sharpe Ratio può essere codificato in Python in questo modo:
def sharpe_ratio(rets):
return rets.mean() / rets.std()
Funzione di trading
Vogliamo usare lo Sharpe Ratio come funzione di ricompensa, ma come usare queste informazioni per fare trading? Usiamo la seguente funzione per determinare la posizione, F, al tempo T:
\(F_t = \tanh(\theta^T x _t)\)
Questa funzione genere un valore compreso tra -1 e 1, che indica la percentuale del portafoglio da dedicare per acquistare o vendere l’asset, \(θ\). Come nel precedente articolo, sono parametri che vogliamo ottimizzare tramite il gradient ascent, e \(x_t\) è il vettore di input per il tempo T.
In questo articolo consideriamo il vettore di input come \(x_t = [1, r_{t – M}, … , r_t, F_{t – 1}]\), dove \(R_t\) è la variazione di valore dell’asset tra il tempo \(t\) e il tempo \(t-1\) e M è il numero di input della serie temporale. In altre parole, in ogni fase temporale forniamo al modello l’ultima posizione e una serie di variazioni storiche dei prezzi che può usare per calcolare la posizione successiva. Possiamo calcolare tutte le posizioni data la serie di prezzi x e theta con la seguente funzione Python:
import numpy as np
def positions(x, theta):
M = len(theta) - 2
T = len(x)
Ft = np.zeros(T)
for t in range(M, T):
xt = np.concatenate([[1], x[t - M:t], [Ft[t - 1]]])
Ft[t] = np.tanh(np.dot(theta, xt))
return Ft
Calcolo dei rendimenti
Ora che sappiamo quale sarà la nostra posizione in ogni fase temporale, possiamo calcolare i nostri rendimenti \(R\) ad ogni istante temporale tramite la seguente formula:
\(R _t = F _{t-1}r _t – \delta | F _t – F _{t – 1}|\)
In questo caso \(\delta\) è il tasso di costo di transazione. Possiamo codificarlo con una funzione in Python come segue:
def returns(Ft, x, delta):
T = len(x)
rets = Ft[0:T - 1] * x[1:T] - delta * np.abs(Ft[1:T] - Ft[0:T - 1])
return np.concatenate([[0], rets])
Questi rendimenti possono essere usati per calcolare lo Sharpe Ratio.
Gradient ascent
Determinare il gradiente
Per eseguire il gradient ascent, dobbiamo calcolare la derivata dello Sharpe Ratio rispetto a theta, o \({dS _T}\over{d\theta}\). Usando la regola della catena e le formule precedenti otteniamo:
\({{dS _T}\over{d\theta}} = \sum\limits_{t=1}^{T} ( {{dS _T}\over{dA}}{{dA}\over{dR _t}} + {{dS _T}\over{dB}}{{dB}\over{dR _t}}) \cdot ({{dR _t}\over{dF _t}}{{dF}\over{d\theta}} + {{dR _t}\over{dF _{t-1}}}{{dF _{t-1}}\over{d\theta}})\)
Per comprendere i passaggi per calcolare la derivata di cui sopra e le derivate parziali, si può consultare l’articolo di Gabriel Molina, Stock Trading with Recurrent Reinforcement Learning (RRL).
Possiamo calcolare questa derivata con la funzione gradient:
def gradient(x, theta, delta):
Ft = positions(x, theta)
R = returns(Ft, x, delta)
T = len(x)
M = len(theta) - 2
A = np.mean(R)
B = np.mean(np.square(R))
S = A / np.sqrt(B - A ** 2)
dSdA = S * (1 + S ** 2) / A
dSdB = -S ** 3 / 2 / A ** 2
dAdR = 1. / T
dBdR = 2. / T * R
grad = np.zeros(M + 2) # inizializza il gradiente
dFpdtheta = np.zeros(M + 2) # memoriiza i dFdtheta precedenti
for t in range(M, T):
xt = np.concatenate([[1], x[t - M:t], [Ft[t - 1]]])
dRdF = -delta * np.sign(Ft[t] - Ft[t - 1])
dRdFp = x[t] + delta * np.sign(Ft[t] - Ft[t - 1])
dFdtheta = (1 - Ft[t] ** 2) * (xt + theta[-1] * dFpdtheta)
dSdtheta = (dSdA * dAdR + dSdB * dBdR[t]) * (dRdF * dFdtheta + dRdFp * dFpdtheta)
grad = grad + dSdtheta
dFpdtheta = dFdtheta
return grad, S
Addestramento del modello
Dopo aver definito la funzione gradiente, possiamo ottimizzare i parametri tramite il gradient ascent. Come nel precedente articolo, aggiorniamo \(\theta\) ad ogni epoca con la formula \(\theta = \theta + \alpha{dS _T \over d\theta}\), dove \(\)\alpha[/latex[ è il learning rate.
def train(x, epochs=2000, M=8, commission=0.0025, learning_rate=0.3):
theta = np.random.rand(M + 2)
sharpes = np.zeros(epochs)
for i in range(epochs):
grad, sharpe = gradient(x, theta, commission)
theta = theta + grad * learning_rate
sharpes[i] = sharpe
print("finished training")
return theta, sharpes
Trading sul Bitcoin
Abbiamo ottenuto un modello che possiamo testare usando i dati storici del bitcoin. Usiamo la cronologia di tutti i trade su bitcoin nell’exchange Bitstamp, scaricata da bitcoincharts.com.
Iniziamo caricando i dati.
import matplotlib.pyplot as plt
plt.rcParams["figure.figsize"] = (5, 3) # (w, h)
plt.rcParams["figure.dpi"] = 150
import pandas as pd
btc = pd.read_csv("bitstampUSD.csv", names=["utc", "price", "volume"]).set_index('utc')
btc.index = pd.to_datetime(btc.index, unit='s')
rets = btc['price'].diff()[1:]
Per questa strategia addestriamo il modello con 1000 campioni e e quindi la testiamo con i successivi 200 campioni. Dividiamo i dati nei dataset di training e di test, quindi li normalizziamo con i dati di training.
x = np.array(rets)
N = 1000
P = 200
x_train = x[-(N+P):-P]
x_test = x[-P:]
std = np.std(x_train)
mean = np.mean(x_train)
x_train = (x_train - mean) / std
x_test = (x_test - mean) / std
Adesso siamo pronti addestrare il modello. Prevediamo una finestra di look-back di 8 tick per il modello.
np.random.seed(0)
theta, sharpes = train(x_train, epochs=2000, M=8, commission=0.0025, learning_rate=0.3)
Per verificare i risultati dell’addestramento, possiamo rappresentare graficamente lo Sharpe Ratio risultante per ogni epoca e vediamo se convergere al massimo.
plt.plot(sharpes)
plt.xlabel('Epoch Number')
plt.ylabel('Sharpe Ratio')
plt.show()
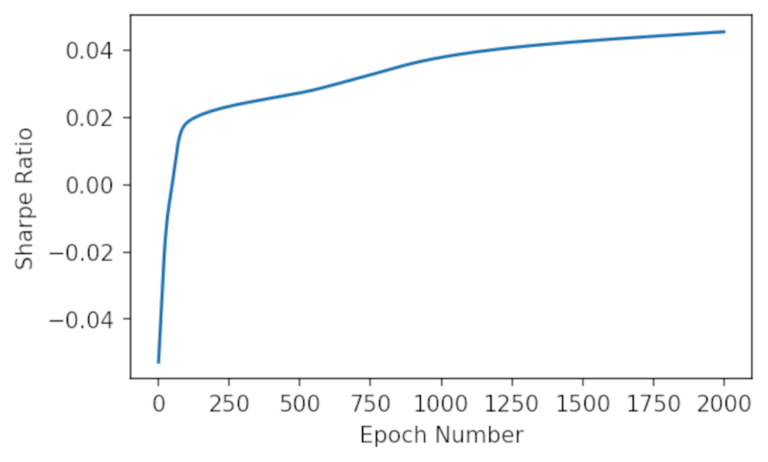
Possiamo vedere che mentre si addestra il modello, si converge verso lo Sharpe Ratio massimo. Vediamo come si è comportato il modello sul dataset di training:
train_returns = returns(positions(x_train, theta), x_train, 0.0025)
plt.plot((train_returns).cumsum(), label="Reinforcement Learning Model", linewidth=1)
plt.plot(x_train.cumsum(), label="Buy and Hold", linewidth=1)
plt.xlabel('Ticks')
plt.ylabel('Cumulative Returns');
plt.legend()
plt.title("RL Model vs. Buy and Hold - Training Data");
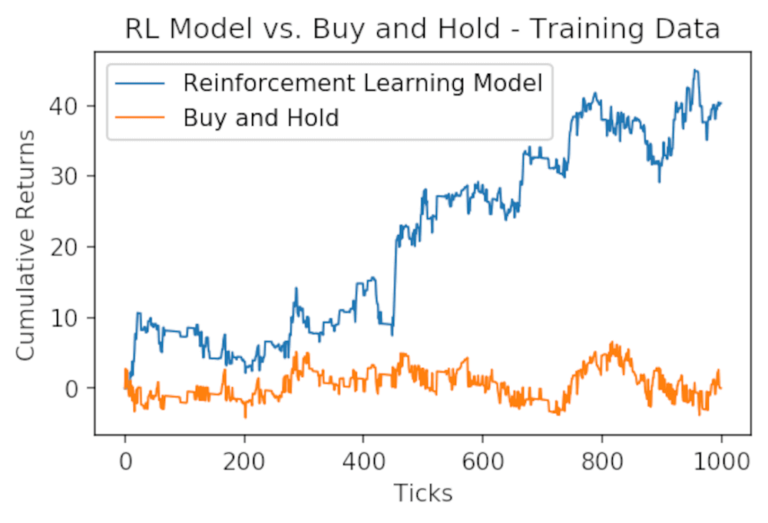
Possiamo vedere che, rispetto ai dati di training, il nostro modello di reinforcement learning ha ampiamente sovraperformato il semplice buy&hold dell’asset. Vediamo come si comporta nei prossimi 200 tick, che sono stati tenuti fuori dal modello.
test_returns = returns(positions(x_test, theta), x_test, 0.0025)
plt.plot((test_returns).cumsum(), label="Reinforcement Learning Model", linewidth=1)
plt.plot(x_test.cumsum(), label="Buy and Hold", linewidth=1)
plt.xlabel('Ticks')
plt.ylabel('Cumulative Returns');
plt.legend()
plt.title("RL Model vs. Buy and Hold - Test Data");
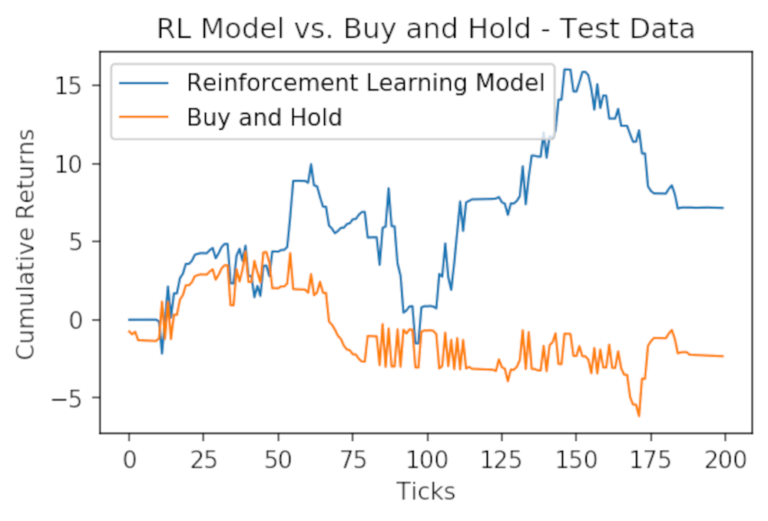
Ancora una volta il modello supera l’asset! Questo modello potrebbe essere migliorato progettando più features (input), ma è un ottimo inizio.
Codice completo
In questo articolo abbiamo descritto un approccio di trading con il reinforcement learning in Python. Per il codice completo riportato in questo articolo, si può consultare il seguente repository di github:
https://github.com/datatrading-info/MachineLearning



