Nel precedente articolo relativo all’analisi delle serie temporali abbiamo descritto l’importanza della correlazione seriale e della sua utilità nel contesto del trading quantitativo.
In questo articolo vediamo come usare la correlazione seriale all’interno dei primi modelli di analisi delle serie temporali, inclusi alcuni semplici modelli stocastici lineari. In particolare, descriviamo il White Noise e Random Walks.
Obiettivo dell'analisi delle serie temporali
Prima di immergerci nelle definizioni, voglio riassumere le nostre motivazioni per studiare questi modelli e il nostro obiettivo finale nello studio dell’analisi delle serie temporali.
Fondamentalmente siamo interessati a migliorare la redditività dei nostri algoritmi di trading. Come analisti quantitativi, non ci basiamo su “supposizioni” o “intuizioni”.
Il nostro approccio consiste nel quantificare il più possibile, sia per rimuovere qualsiasi coinvolgimento emotivo dal processo di trading sia per garantire (per quanto possibile) la ripetibilità del nostro trading.
Al fine di migliorare la redditività dei nostri modelli di trading, dobbiamo utilizzare tecniche statistiche per identificare comportamenti coerenti in specifici strumenti che possono essere sfruttati per realizzare un profitto. Per trovare questo comportamento dobbiamo esplorare come le proprietà dei prezzi degli asset cambiano nel tempo.
L’analisi delle serie temporali ci aiuta a raggiungere questo obiettivo. Ci fornisce un solido quadro statistico per valutare il comportamento delle serie temporali, come i prezzi degli asset, al fine di aiutarci a definire una strategia che sfrutti questo comportamento.
L’analisi delle serie temporali ci fornisce un solido quadro statistico per valutare il comportamento dei prezzi degli asset.
Finora abbiamo discusso la correlazione seriale ed esaminato la struttura di correlazione di base dei dati simulati. Inoltre abbiamo definito la stazionarietà e considerato le proprietà di secondo ordine delle serie temporali. Tutti questi attributi ci aiuteranno a identificare i modelli tra le serie temporali. Se non hai letto l’articolo precedente sulla correlazione seriale , ti consiglio caldamente di farlo prima di continuare con questo articolo.
Di seguito esamineremo come possiamo sfruttare parte della struttura dei prezzi degli asset che abbiamo identificato utilizzando modelli di serie temporali .
Processo di modellazione delle serie storiche
Allora, cos’è un modello di una serie temporale? Essenzialmente, è un modello matematico che tenta di “spiegare” la correlazione seriale presente in una serie temporale.
Con il termine “spiega” si intende che il modello “adattato” ad una serie temporale dovrebbe tenere conto di alcune o tutte le correlazioni seriali presenti nel correlogramma. Cioè, adattando il modello a una serie storica, stiamo riducendo la correlazione seriale.
Il nostro processo, come ricercatori quantitativi, consiste nel considerare un’ampia varietà di modelli, comprese le loro ipotesi e la loro complessità, e quindi scegliere un modello in modo tale che sia quello “più semplice” per spiegare la correlazione seriale.
Una volta che abbiamo definito tale modello, possiamo usarlo per prevedere i valori futuri o, più in generale, il comportamento futuro. Questa previsione è ovviamente estremamente utile nel trading quantitativo.
Se possiamo prevedere la direzione del movimento di un asset, allora abbiamo la base di una strategia di trading (tenendo ovviamente conto dei costi di transazione!). Inoltre, se possiamo prevedere la volatilità di un asset, allora abbiamo la base per un’altra strategia di trading o per un approccio di gestione del rischio. Questo è il motivo per cui siamo interessati alle proprietà di secondo ordine, poiché fornisco i mezzi per aiutarci a fare previsioni.
Una domanda da porsi in questi casi è “Come facciamo a sapere quando abbiamo una buona misura per un modello?”. Quali criteri utilizziamo per giudicare quale modello è il migliore? In effetti, ce ne sono diversi! Considereremo questi criteri in questa serie di articoli.
Riassumiamo il processo generale che seguiremo in tutta la serie:
- Delineare un’ipotesi su una particolare serie temporale e sul suo comportamento
- Ottenere il correlogramma delle serie temporali (utilizzando le librerie Python) e valutare la sua correlazione seriale
- Utilizzare la nostra conoscenza dei modelli di serie temporali e adattare un modello appropriato per ridurre la correlazione seriale nei residui (vedi sotto per una definizione) del modello e delle sue serie temporali
- Affinare l’adattamento fino a quando non ci sono più correlazioni e utilizzare i criteri matematici per valutare l’adattamento del modello
- Utilizzare il modello e le sue proprietà di secondo ordine per fare previsioni sui valori futuri
- Valutare l’accuratezza di queste previsioni utilizzando tecniche statistiche (come matrici di confusione , curve ROC per la classificazione o metriche regressive come MSE , MAPE ecc.)
- Iterare questo processo fino a quando la precisione è ottimale e quindi utilizzare tali previsioni per creare strategie di trading
Questo è il nostro processo di base. La complessità sorgerà quando considereremo modelli più avanzati che tengono conto di correlazioni seriali aggiuntive nelle nostre serie temporali.
In questo articolo prenderemo in considerazione due dei modelli di serie temporali più basilari, ovvero il White Noise e Random Walks. Questi modelli formeranno la base dei seguenti modelli più avanzati, quindi è essenziale comprenderli nei dettagli.
Tuttavia, prima di introdurre uno di questi modelli, descriviamo alcuni concetti più astratti che ci aiuteranno a unificare il nostro approccio ai modelli delle serie temporali. In particolare, definiremo l’operatore di spostamento all’indietro e l’ operatore di differenza .
Operatori di spostamento all'indietro e di differenza
L’operatore di spostamento all’indietro (BSO) e l’operatore di differenza ci consentono di scrivere molti differenti modelli di serie temporali in uno specifico modo che ci aiuta a capire come differiscono l’uno dall’altro.
Dal momento che useremo queste notazioni molto frequentemente, ha senso definirli ora.
Operatore di spostamento all’indietro
L’ operatore di spostamento all’indietro o di ritardo , \({\bf B}\), accetta un elemento della serie temporale come argomento e restituisce l’elemento in un’unità di tempo precedente: \({\bf B} x_t = x_ {t-1} \).
L’applicazione ripetuta dell’operatore ci permette di tornare indietro di \(n\) volte: \({\bf B} ^ n x_t = x_{tn} \).
In futuro utilizzeremo il BSO per definire molti dei nostri modelli di serie temporali.
Inoltre, quando si arriva a studiare modelli di serie temporali che non sono stazionari (cioè, la loro media e varianza possono cambiare nel tempo), possiamo usare una procedura di differenziazione per prendere una serie non stazionaria e produrre una serie stazionaria.
Operatore differenza
L’operatore differenza , \( \nabla \), accetta un elemento della serie temporale come argomento e restituisce la differenza tra l’elemento e quello di un’unità di tempo precedente: \(\nabla x_t = x_t – x_{t-1} \) o \(\nabla x_t = (1 – {\bf B}) x_t \).
Come con BSO, possiamo applicare ripetutamente l’operatore di differenza: \( \nabla ^ n = (1 – {\bf B})^n \).
Ora che abbiamo discusso di questi operatori astratti, consideriamo alcuni modelli concreti di serie temporali.
White Noise
Cominciamo cercando di motivare il concetto di rumore bianco.
In precedenza, abbiamo descritto che il nostro approccio di base consiste nel provare ad adattare i modelli a una serie temporale fino a quando le serie rimanenti non presentano alcuna correlazione seriale. Ciò motiva la definizione della serie degli errori residui:
Serie dei residui
La serie degli errori residui(o residui), \(x_t\), è una serie temporale della differenza tra un valore osservato e un valore previsto, da un modello di serie temporale, in un determinato momento \(t\).
Se \(y_t\) è il valore osservato e \(\hat{y}_t \) è il valore previsto, diciamo: \(x_t = y_t – \hat{y}_t \) sono i residui.
Il punto chiave è verificare se il modello di serie temporale scelto è in grado di “spiegare” la correlazione seriale nelle osservazioni, allora gli stessi residui sono serialmente non correlati.
Questo significa che ogni elemento della serie dei residui non correlati serialmente è una realizzazione indipendente di una specifica distribuzione di probabilità. In altre parole, gli stessi residui sono indipendenti e distribuiti in modo identico (iid).
Quindi, se vogliamo creare modelli di serie temporali che spieghino qualsiasi correlazione seriale, è naturale iniziare con un processo che produce variabili casuali indipendenti da una certa distribuzione. Questo porta direttamente al concetto di rumore bianco (discreto):
Rumore bianco discreto
Si consideri una serie temporale \( \{w_t: t=1,…n\}\). Se gli elementi della serie, \( w_i \), sono indipendenti e distribuiti in modo identico (iid), con media zero, varianza \( \sigma^2 \) e nessuna correlazione seriale (cioè \( \text {Cor} (w_i, w_j) \neq 0, \forall i \neq j \)) allora diciamo che la serie temporale è un rumore bianco discreto (DWN).
In particolare, se i valori \( w_i \) sono tratti da una distribuzione normale standard (cioè \( w_t \sim N (0, \sigma^2) \)), la serie è nota come Rumore bianco gaussiano .
Il White Noise è utile in molti contesti. In particolare, può essere utilizzato per simulare una serie “sintetica” .
Come accennato in precedenza, una serie temporale storica è solo un’istanza osservata. Se siamo in grado di simulare più realizzazioni, allora possiamo creare “molte storie” e quindi generare statistiche per alcuni dei parametri di modelli particolari. Questo ci aiuterà a perfezionare i nostri modelli e quindi ad aumentare la precisione nelle nostre previsioni.
Ora che abbiamo definito il Discrete White Noise, esamineremo alcuni dei suoi attributi, incluse le sue proprietà di secondo ordine e il suo correlogramma.
Proprietà di secondo ordine
Le proprietà di secondo ordine del DWN sono semplici e facilmente intuibili dalla sua definizione. In particolare, la media delle serie è zero e non c’è autocorrelazione per definizione
\(\begin{eqnarray} \mu_w = E(w_t) = 0 \end{eqnarray}\)
\(\rho_k = \text{Cor}(w_t, w_{t+k}) = \left\{\begin{aligned} &1 && \text{if} \enspace k = 0 \\ &0 && \text{if} \enspace k \neq 0 \end{aligned} \right.\)
Correlogramma
Possiamo anche tracciare il correlogramma di un DWN usando Python. Per prima cosa definiamo un seed casuale pari a 1, in modo le estrazioni casuali siano identiche per ogni lancio dello script. Quindi campioniamo 1000 elementi da una distribuzione normale e tracciamo l’autocorrelazione:
import numpy as np
from matplotlib import pyplot as plt
from statsmodels.graphics.tsaplots import plot_acf
from statsmodels.tsa.stattools import acf
np.random.seed(1)
whiteNoise = np.random.standard_normal(1000)
acf_coef = acf(whiteNoise)
plot_acf(acf_coef, lags=30)
plt.show()
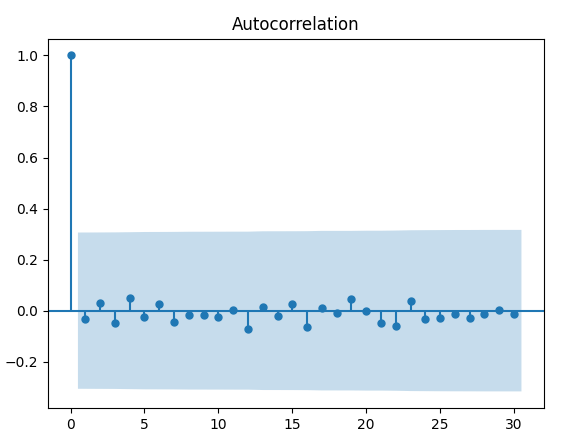
Si noti che a \( k = 4 \), \( k = 12 \) e \( k = 16 \), abbiamo tre picchi che differiscono da zero per un livello del 5%. Tuttavia, questo è facilmente prevedibile a causa della variazione del campionamento dalla distribuzione normale.
Ancora una volta, dobbiamo essere estremamente attenti nella nostra interpretazione dei risultati. In questo caso, ci aspettiamo davvero che accada qualcosa di fisicamente significativo per \( k = 4 \), \( k = 12 \) o \( k = 16 \)?
Si noti che il modello DWN ha un solo parametro, vale a dire la varianza \( \sigma^2 \). Per fortuna, è semplice stimare la varianza con Python, possiamo semplicemente usare la funzione var della libreria Numpy:
var = np.var(whiteNoise)
print(var)
Dato che abbiamo specificamente definito il white noise come una distribuzione normale (quindi con una media pari a 0 e una deviazione standard pari a 1 (e quindi una varianza di 1). Python calcola la varianza del campionaria come 0.962369, che è vicino al valore ideale di 1.
Il Discrete White Noise è fondamentalmente usato come modello per i residui . Stiamo cercando di adattare altri modelli di serie temporali alle nostre serie osservate, a quel punto utilizziamo il DWN come conferma che abbiamo eliminato qualsiasi correlazione seriale rimanente dai residui e quindi abbiamo un buon adattamento del modello.
Ora che abbiamo esaminato il DWN, descriviamo un modello famoso per (alcune) serie temporali finanziarie, ovvero il Random Walk.
Random Walks
Una passeggiata casuale è un altro modello di serie temporale in cui l’osservazione corrente è uguale all’osservazione precedente con un incremento o decremento casuale. È formalmente definito come segue:
Passeggiata casuale
Una passeggiata casuale è un modello di serie temporale \( {x_t} \) tale che \( x_t = x_ {t-1} + w_t \), dove \( w_t \) è una serie di rumore bianco discreto.
In precedenza abbiamo definito l’operatore di spostamento all’indietro \( {\bf B} \). Possiamo applicare il BSO alla passeggiata casuale:
\(\begin{eqnarray} x_t = {\bf B} x_t + w_t = x_ {t-1} + w_t \end{eqnarray}\)
E facendo un ulteriore passo indietro:
\( \begin{eqnarray} x_{t-1} = {\bf B} x_{t-1} + w_{t-1} = x_{t-2} + w_{t-1} \end{eqnarray}\)
Se ripetiamo questo processo fino alla fine della serie temporale otteniamo
\(\begin{eqnarray} x_t = (1 + {\bf B} + {\bf B}^2 + \ldots) w_t \end{eqnarray}\)
da cui
\( x_t = w_t + w_{t-1} + w_{t-2} + \ldots\)
Quindi è chiaro come la passeggiata aleatoria sia semplicemente la somma degli elementi di una serie di rumore bianco discreto.
Proprietà di secondo ordine
Le proprietà di secondo ordine di una passeggiata aleatoria sono un po ‘più interessanti di quelle del rumore bianco discreto. Sebbene la media di una passeggiata aleatoria sia ancora zero, la covarianza è in realtà dipendente dal tempo. Quindi una passeggiata aleatoria non è stazionaria:
\(\begin{eqnarray}\mu_x &=& 0 \\ \gamma_k (t) &=& \text{Cov}(x_t, x_{t+k}) = t \sigma^2 \end{eqnarray}\)
In particolare, la covarianza è uguale alla varianza moltiplicata per il tempo. Quindi, con l’aumentare del tempo, aumenta anche la varianza.
Cosa significa questo per passeggiate casuali? In parole povere, significa che non ha molto senso estrapolare “trend” a lungo termine, poiché sono letteralmente processi casuali .
Correlogramma
L’autocorrelazione di una passeggiata casuale (che è anch’essa dipendente dal tempo) può essere definita come segue:
\(\begin{eqnarray} \rho_k (t) = \frac{\text{Cov}(x_t, x_{t+k})} {\sqrt{\text{Var}(x_t) \text{Var}(x_{t+k})}} = \frac{t \sigma^2}{\sqrt{t \sigma^2 (t+k) \sigma^2}} = \frac{1}{\sqrt{1+k/t}} \end{eqnarray}\)
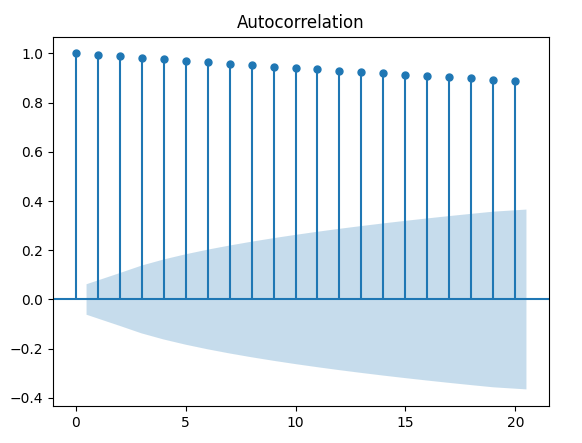
Quindi se si considera una lunga serie temporale, con ritardi a breve termine, allora otteniamo un’autocorrelazione quasi unitaria. Cioè, abbiamo un’autocorrelazione estremamente elevata che non diminuisce molto rapidamente all’aumentare del ritardo. Possiamo simulare una serie del genere usando Python.
In primo luogo, definiamo il seed in modo che si possa replicare esattamente gli stessi risultati. Quindi creiamo due sequenze di estrazioni casuali (\( x \) e \( w \)), ognuna delle quali ha lo stesso valore (come definito dal seed).
Quindi eseguiamo un ciclo attraverso ogni elemento di \( x \) e gli assegniamo il valore dell’elemento precedente di \( x \) più il valore corrente di \( w \). In questo modo ricaviamo una passeggiata casuale. Quindi tracciamo i risultati usando type="l"per darci un grafico a linee, piuttosto che un grafico di punti circolari:
from statsmodels.graphics.tsaplots import plot_acf
from statsmodels.tsa.arima_process import ArmaProcess
from statsmodels.tsa.stattools import acf
import matplotlib.pyplot as plt
import numpy as np
np.random.seed(1)
steps = np.random.standard_normal(1000)
steps[0] = 0
random_walk = np.cumsum(steps)
plt.figure(figsize=[10, 7.5]); # Dimensioni del grafico
plt.plot(random_walk)
plt.title("Simulated Random Walk")
plt.show()
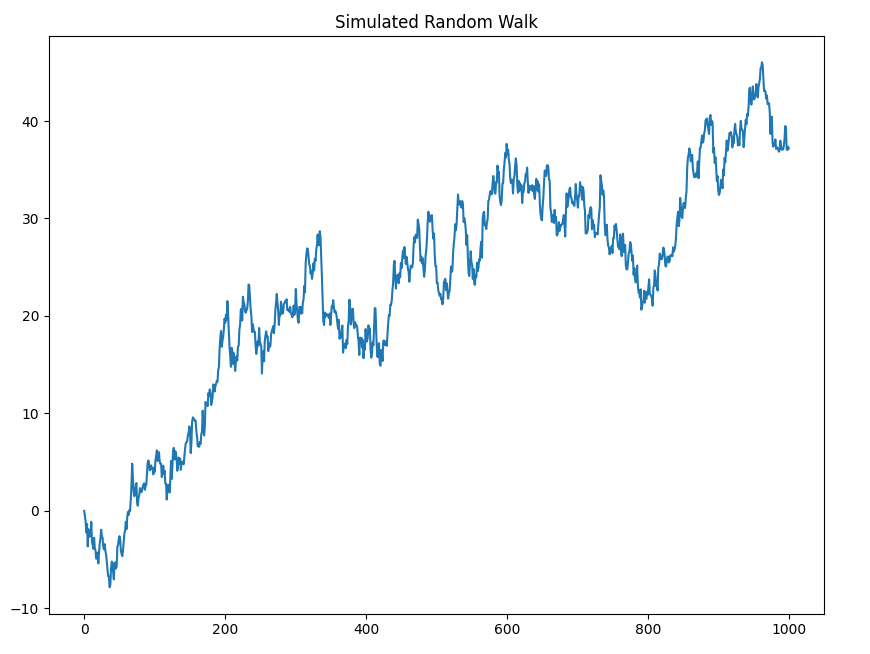
È anche abbastanza semplice disegnare il correlogramma:
random_walk_acf_coef = acf(random_walk)
plot_acf(random_walk, lags=20);
plt.show()
Adattamento dei Modelli di Random Walk ai dati Finanziari
Come descritto nell’articolo precedente, è quindi necessario adattare i modelli ai dati che abbiamo già simulato.
Chiaramente questo è un po’ artificioso, dato che abbiamo simulato anche la random walk. Tuttavia, è utile come semplice descrizione delle basi del processo di adattamento . In situazioni reali non conosceremo il modello di generazione per i dati dello strumento sottostante, possiamo solamente adattare i modelli e quindi valutarne il correlogramma.
Abbiamo affermato come questo processo è utile per semplificare il processo di verifica della corretta implementazione del modello, cercando di garantire che le stime dei parametri siano vicine a quelle utilizzate nelle simulazioni.
Adattamento ai dati simulati
Dato che impiegheremo molto tempo ad adattare i modelli alle serie temporali finanziarie, dovremmo prima fare pratica sui dati simulati, in modo da avere pratica del processo quando si inizia a utilizzare i dati reali.
Abbiamo già simulato una random walk aleatoria, quindi possiamo anche usare quella realizzazione per vedere se il modello proposto (per un processo aleatorio) è accurato.
Come possiamo sapere se il modello ipotizzato per la random walk è adatto per i nostri dati simulati? Bene, facciamo uso della definizione di un processo aleatorio, quindi si prevede che la differenza tra due valori vicini è uguale possa essere descritto da un processo di rumore bianco discreto.
Quindi, se creiamo una serie di differenze di elementi dalla nostra serie simulata, dovremmo avere una serie che assomigli al rumore bianco discreto!
In Python è semplicemente implementato tramite l’uso della funzione diff. Dopo aver creato la serie ellei differenze, si stampa il grafico del correlogramma e quindi valutare quanto sia vicino al rumore bianco discreto:
random_walk_diff = np.diff(random_walk, n=1)
random_walk_diff_acf_coef = acf(random_walk_diff)
plot_acf(random_walk_diff, lags=20);
plt.show()
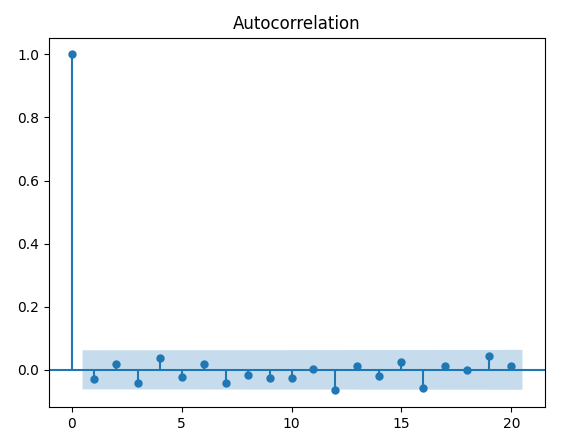
Cosa possiamo notare da questo grafico? C’è un picco statisticamente significativo per \( k = 12 \), ma solo marginalmente. Da ricordare che ci si aspettiamo di avere almeno il 5% dei picchi che sono statisticamente significativi, a causa della variazione del campionamento.
Quindi possiamo ragionevolmente affermare che il correlogramma assomiglia a quello del rumore bianco discreto. Ciò implica che il modello di random walk si adatta bene ai nostri dati simulati. Questo è esattamente quello che dovremmo aspettarci, dal momento che abbiamo inizialmente simulato una random walk!
Adattamento ai dati finanziari
Applichiamo ora il nostro modello di random walk ad alcuni effettivi dati finanziari. Tramite la libreria Python, pandas, possiamo usare il pacchetto Pandas Datareader per ottenere facilmente i dati finanziari tramite Yahoo Finance.
Vedremo se un modello di passeggiata aleatoria è adatto per alcuni dati azionari. In particolare, sceglierò Microsoft (MSFT), ma puoi sperimentare con il tuo ticker preferito!
Prima di poter scaricare qualsiasi dato, dobbiamo installare il pacchetto pandas-datareader poiché non fa parte dell’installazione predefinita di Pandas. E’ sufficiente eseguire il seguente comando:
pip install pandas-datareader
E’ quindi possibile scaricare i dati di MSFT con una semplice chiamata ad una funzione di pandas-datareader
mstf = pdr.get_data_yahoo('MSFT', start='01/01/2000', end='08/01/2017')
msft dove possiamo accedere alla serie dei prezzi di chiusura aggiustati per lo specifico titolo azionario.
Il nostro processo consisterà nel calcolare la differenza dei valori di chiusura, omettere eventuali valori mancanti e quindi applicarli alla funzione di autocorrelazione. Quando tracciamo il correlogramma, cerchiamo prove della presenza di rumore bianco discreto, ovvero una serie di residui non correlata in modo seriale. Per eseguire ciò in Python, eseguiamo il seguente comando:
mstf_close = mstf['Adj Close']
msft_diff = np.diff(mstf_close, n=1)
msft_diff_acf_coef = acf(msft_diff,missing="drop")
plot_acf(msft_diff_acf_coef, lags=20)
plt.show()
L’ultima parte (missing = "drop") specifica alla funzione acf di ignorare i valori NaN. L’output della funzioneacf è il seguente:
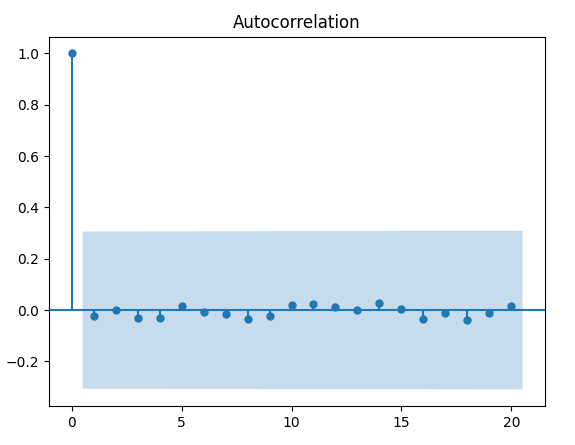
Notiamo che la maggior parte dei picchi di lag non differisce dallo zero per più del 5%. Tuttavia ce ne sono alcuni che sono marginalmente superiori. Dato che i ritardi \( k_i \) per i quali si verifica un picco anomalo sono indipendenti da \( k = 0 \), potremmo essere inclini a pensare che questi siano causati da variazioni stocastiche e non rappresentino alcuna correlazione seriale presente nella serie.
Quindi possiamo concludere, con un ragionevole grado di certezza, che i prezzi di chiusura rettificati di MSFT sono ben approssimati da una random walk.
Proviamo ora lo stesso approccio sullo stesso indice S&P500. Il simbolo Yahoo Finance per l’S&P500 è ^GSPC. Quindi, se inseriamo i seguenti comandi in Python, possiamo tracciare il correlogramma della serie di differenze dell’S & P500:
sp500 = pdr.get_data_yahoo('^GSPC', start='01/01/2000', end='08/01/2017')
sp500_close = sp500['Adj Close']
sp500_diff = np.diff(sp500_close, n=1)
sp500_diff_acf_coef = acf(sp500_diff,missing="drop")
plot_acf(sp500_diff_acf_coef, lags=20)
plt.show()
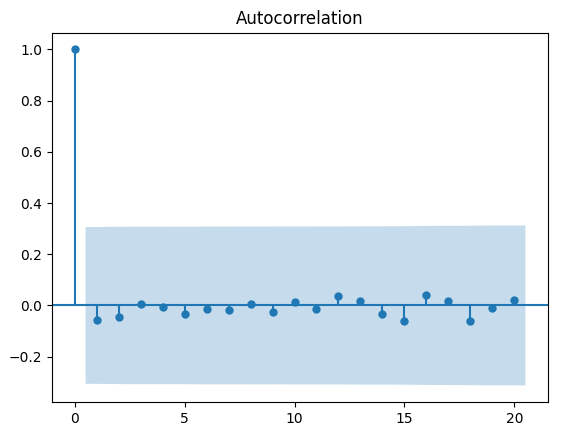
Questo correlogramma è sicuramente più interessante. Si noti che esiste una correlazione negativa per \( k = 1 \). È improbabile che ciò sia dovuto alla variazione casuale del campionamento.
Da notare anche che ci sono picchi per \( k = 2 \), \( k = 15 \) e \( k = 18 \). Sebbene sia più difficile giustificare la loro esistenza oltre a quella della variazione casuale, possono essere indicativi di un processo di ritardo più lungo.
Quindi è molto più difficile giustificare una random walk come un buon modello per la serie dei prezzi di chiusura aggiustati dell’S&P500. Quindi dobbiamo usare modelli più sofisticati, vale a dire i modelli di ordine autoregressivo p , che sarà l’argomento del prossimo articolo!