Le tre principali aree di lavoro di un trader sistematico, cioè lo scripting, il backtest e l’ottimizzazione delle strategie. In questo articolo le esaminiamo tutte e tre contemporaneamente, insieme al concetto del multi-threading nel backtest di strategie sistematiche per velocizzare e ottimizzare il lavoro.
Vediamo come implementare gli script, uno operante in modalità multi-thread e l’altro a thread singolo, per effettuare le seguenti attività:
- Scrivere il codice per eseguire il backtest simulato di una semplice strategia di media mobile.
- Eseguire l’ottimizzazione della strategia con un approccio a forza bruta sui parametri di input, cioè i due periodi della media mobile. Si registra lo Sharpe Ratio di ogni esecuzione, e quindi si analizza i dati relativi allo Sharpe massimo.
- Ad ogni esecuzione dell’ottimizzazione, le serie dei rendimento e della volatilità del backtest sono usati da a una funzione che esegue l’analisi Monte Carlo e produce una distribuzione di possibili risultati per quel particolare insieme di input. Probabilmente è eccessivo l’eseguire l’analisi Monte Carlo per i risultati di ogni backtest, ma è utile per mostrare come eseguire il multithreading di un processo e i vantaggi che si possono ottenere in termini di tempo di esecuzione del codice. Non vogliamo analizzare l’output dei backtest.
Per iniziare dobbiamo recuperare una serie storica dei prezzi di un titolo azionario. In questo articolo usiamo la serie dei prezzi giornalieri di Ford (FN) che sono disponibili al seguente link: F.csv
Dopo aver acquisito in un dataframe i dati sui prezzi giornalieri per Ford (FN) dalla metà del 1972 in poi, dovrebbe apparire come segue:
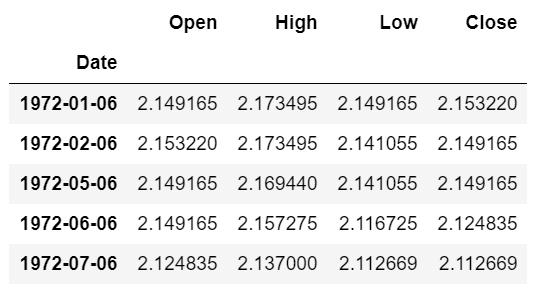
Approccio con thread singolo
Per capire il multi-threding nel backtest di strategie di trading, vediamo innanzitutto il codice per eseguire in un singolo thread le attività descritti in precedenza. Per prima cosa importiamo i moduli necessari:
import numpy as np
import pandas as pd
import itertools
import time
Successivamente definiamo una funzione di supporto per calcolare lo Sharpe Ratio annualizzato dei rendimenti risultanti da un backtest.
# Funzione per calcolare lo Sharpe Ratio
def annualised_sharpe(returns, N=252):
if returns.std() == 0:
return 0
return np.sqrt(N) * (returns.mean() / returns.std())
data, short_ma e long_ma. I “dati” sono i dati dei prezzi usati per testare la strategia, mentre gli altri due parametri sono le lunghezze dei due periodi delle media mobile.
def ma_strat(data, short_ma, long_ma):
# Calcolo dei valori delle SMA
data['short_ma'] = np.round(data['Close'].rolling(window=short_ma).mean(),2)
data['long_ma'] = np.round(data['Close'].rolling(window=long_ma).mean(),2)
# Calcolo dello spread delle medie mobili
data['short_ma-long_ma'] = data['short_ma'] - data['long_ma']
# Imposta il numero di punti come soglia dello spread e
# calcolo dello ''Stance' della strategia
X = 5
data['Stance'] = np.where(data['short_ma-long_ma'] > X, 1, 0)
data['Stance'] = np.where(data['short_ma-long_ma'] < -X, -1, data['Stance'])
data['Stance'].value_counts()
# Calcolo dei rendimenti logaritmici giornalieri per i prezzi e per la strategia
data['Market Returns'] = np.log(data['Close'] / data['Close'].shift(1))
data['Strategy'] = data['Market Returns'] * data['Stance'].shift(1)
# Calcolo della curva equity
data['Strategy Equity'] = data['Strategy'].cumsum()
# Calcolo dello Sharpe Ratio
try:
sharpe = annualised_sharpe(data['Strategy'])
except:
sharpe = 0
return data['Strategy'].cumsum(), sharpe, data['Strategy'].mean(), data['Strategy'].std()
Successivamente definiamo una terza funzione che esegue il backtest della strategia MA e le simulazioni Monte Carlo per ogni possibile valore dei parametri di input della strategia. La funzione prevede 3 argomenti: “data”, “input” e “iter”. data è la serie dei prezzi. inputs è una tupla con 2 valori appartenenti all’elenco di combinazioni di lunghezze previste per le medie mobili. iters è il numero di simulazioni Monte Carlo che vogliamo eseguire per ogni risultato di ottimizzazione del backtest.
def monte_carlo_strat(data, inputs, iters):
# Numero di giorni per ogni simulazione Monte Carlo
days = 252
# Backtest della strategia con i parametri della funzione
# e memorizzazione dei risultati
perf, sharpe, mu, sigma = ma_strat(data, inputs[0], inputs[1])
# Crea 2 liste vuote per memorizzare i risultati delle simulazioni MC
mc_results = []
mc_results_final_val = []
# Esegue il numero di simulazione MC e memorizza i risultati
for j in range(iters):
daily_returns = np.random.normal(mu, sigma, days) + 1
price_list = [1]
for x in daily_returns:
price_list.append(price_list[-1] * x)
# Memorizza la serie dei prezzi di ogni simulazione
mc_results.append(price_list)
# Memorizza solo il valore finale di ogni serie di prezzi
mc_results_final_val.append(price_list[-1])
return (inputs, perf, sharpe, mu, sigma, mc_results, mc_results_final_val)
Infine dobbiamo acquisire i dati dei prezzi su cui vogliamo eseguire il backtest, generare le combinazioni di input per i periodi delle medie mobile che vogliamo testare e quindi eseguire la funzione per ogni set di input. Cronometriamo i tempi di esecuzione del processo e stampiamo il numero di secondi impiegati.
if __name__ == '__main__':
# Legge i dati dei prezzi
data = pd.read_csv('F.csv', index_col='Date', dayfirst=True, parse_dates=True)
# Genera la lista dei possibili valori per la media mobile breve
short_mas = np.linspace(20, 50, 30, dtype=int)
# Genera la lista dei possibili valori per la media mobile lunga
long_mas = np.linspace(100, 200, 30, dtype=int)
# Genera la lista di tuple che contengono tutte le possibile combinazioni
# dei periodi delle medie mobili
mas_combined = list(itertools.product(short_mas, long_mas))
# Numero di simulazioni MC per l'ottimizzazione dei backtest
iters = 2000
# Crea una lista vuota
results = []
# tempo di inizio
start_time = time.time()
# iterazione attraverso la lista dei valori per le MA ed esegue la funzione
for inputs in mas_combined:
res = monte_carlo_strat(data, inputs, iters)
results.append(res)
# Stampa il numero di secondi impiegati dal processo
print("MP--- %s seconds for single---" % (time.time() - start_time))
Otteniamo il seguente risultato.
MP--- 388.3300528526306 seconds for single---
Abbiamo impiegato tra i 6 minuti e i 7 minti per eseguire 30 x 30 = 900 backtest, dove per ogni backtest abbiamo effettuato una simulazione Monte Carlo con 2000 iterazioni, con ogni iterazione che calcola 252 giorni di rendimenti giornalieri. Non è male considerando che i dati sui prezzi delle azioni Ford che abbiamo usato coprono un periodo di 11.820 giorni. Ciò equivale al calcolo di moltissimi rendimenti giornalieri!! Secondo i miei calcoli abbiamo effettuata elaborato circa 464.238.000 valori di rendimenti giornalieri , come segue:
- esecuzione dei backtest = 30 x 30 = 900
- rendimenti giornalieri calcolati durante i backtest = 900 x 11.820 = 10.638.000
- rendimenti giornalieri calcolati durante le simulazioni Monte Carlo = 900 x 2000 x 252 = 453.600.000
Approccio con multi-thread
Possiamo concludere che aspettare 6 minuti è accettabile per produrre una quantità così grande di dati simulati. Tuttavia… con un po’ di lavoro possiamo ridurre di molto il tempo di esecuzione con un approccio multi-threading nel backtest di strategie di trading. Dobbiamo modificare il codice e aggiungere un paio di funzioni intermedie.
La prima cosa che dobbiamo fare è aggiungere alcune importazioni extra, quindi ora il nostro codice è simile al seguente:
import numpy as np
import pandas as pd
import itertools
from multiprocessing.pool import ThreadPool as Pool
import time
Definiamo un’altra semplice funzione di supporto che permette di prendere la lista di tuple dei valori a media mobile e suddividerla in una serie di liste più piccole con una lunghezza a nostra scelta.
def chunk(it, size):
it = iter(it)
return iter(lambda: tuple(itertools.islice(it, size)), ())
Non prevediamo modifiche alla funzione di backtest ma_strat(). Dobbiamo invece prevede un paio di modifiche alla funzione monte_carlo_strat(). Con l’approccio multi-threading dobbiamo passare alla funzione una parte dell’intera lista contenente più coppie di tuple, invece di passare una sola tupla alla volta. Nel nostro caso ogni insieme contiene 180 coppie di tuple. Iteriamo questa “fetta” di coppie di tuple e per ognuna tupla eseguiamo un backtest, una simulazione Monte Carlo (composta da 2000 iterazioni dove ciascuna simula 252 giorni) e memorizziamo i risultati di ogni iterazione.
def monte_carlo_strat(data, inputs, iters):
# Numero di giorni per ogni simulazione Monte Carlo
days = 252
# Ciclo attraverso un sottoinsieme della lista delle tuple
for input_slice in inputs:
# Backtest della strategia con i parametri della funzione
# e memorizzazione dei risultati
perf, sharpe, mu, sigma = ma_strat(data, input_slice[0], input_slice[1])
# Crea 2 liste vuote per memorizzare i risultati delle simulazioni MC
mc_results = []
mc_results_final_val = []
# Esegue il numero di simulazione MC e memorizza i risultati
for j in range(iters):
daily_returns = np.random.normal(mu, sigma, days) + 1
price_list = [1]
for x in daily_returns:
price_list.append(price_list[-1] * x)
# Memorizza la serie dei prezzi di ogni simulazione
mc_results.append(price_list)
# Memorizza solo il valore finale di ogni serie di prezzi
mc_results_final_val.append(price_list[-1])
return (inputs, perf, sharpe, mu, sigma, mc_results, mc_results_final_val)
Successivamente dobbiamo creare la funzione che permette di generare più thread e gestirli correttamente. Per questo attingiamo al modulo “multiprocessing” e in particolare alla classe ThreadPool. La funzione si scrive così:
def parallel_monte_carlo(data, inputs, iters):
pool = Pool(5)
future_res = [pool.apply_async(monte_carlo_strat, args=(data, inputs[i], iters)) for i in range(len(inputs))]
samples = [f.get() for f in future_res]
return samples
Questa funzione genera 5 thread e li usa per eseguire la funzione contemporaneamente attraverso blocchi della lista di input, ovvero la lista delle tuple dei valori dei periodi per le medie mobili. I risultati sono memorizzati nella variabile future_res che a sua volta deve essere estratta in una lista utilizzando il metodo .get(). La funzione restituisce i risultati del campione.
Dobbiamo aggiungere un altro blocco di codice, l’equivalente del blocco finale nell’esempio di “single thread”. Questa volta è però leggermente diverso..
if __name__ == '__main__':
# Legge i dati dei prezzi
data = pd.read_csv('F.csv', index_col='Date', dayfirst=True, parse_dates=True)
# Genera la lista dei possibili valori per la media mobile breve
short_mas = np.linspace(20, 50, 30, dtype=int)
# Genera la lista dei possibili valori per la media mobile lunga
long_mas = np.linspace(100, 200, 30, dtype=int)
# Genera la lista di tuple che contengono tutte le possibile combinazioni
# dei periodi delle medie mobili
mas_combined = list(itertools.product(short_mas, long_mas))
# Usa la funzione per dividere la lista delle tuple dei periodi di MA in gruppi di 180 tuple
mas_combined_split = list(chunk(mas_combined, 180))
# Numero di simulazioni MC per l'ottimizzazione dei backtest
iters = 2000
# Tempo di inizio
start_time = time.time()
# Chiamata alla funzione di multi-threaded
results = parallel_monte_carlo(data, mas_combined_split, iters)
# Stampa il numero di secondi impiegati dal processo
print("MP--- %s seconds for para---" % (time.time() - start_time))
Otteniamo il seguente risultato.
MP--- 109.21702361106873 seconds for para---
Non è male! Il tempo impiegato è sceso dai quasi 7 minuti a poco meno di 2 minuti.
Da notare che la riduzione del tempo di esecuzione del codice non è un dato di fatto. E’ un risultato specifico per la scelta degli input che abbiamo inserito. C’è un compromesso in termini di velocità che si ottiene eseguendo i thread contemporaneamente e il tempo impiegato per generare quei thread e gestirli in background ecc. Ma so che esiste un compromesso… la migliore prestazione è raggiunta quando il processo in esecuzione su ciascun thread è il principale uso di tempo/risorse dell’intero processo. Se il processo che viene passato a un nuovo thread richiede un tempo relativamente breve per essere eseguito, il vantaggio che otteniamo è superato dal tempo impiegato per generare e gestire il thread .
Dobbiamo quindi giocare con gli input e verificare il tipo di risultati ottenuti. Per il momento lasciamo al lettore il compito di estrarre e analizzare i risultati, per vedere se riuscite a fare un po’ di pratica.
Codice completo
In questo articolo abbiamo descritto come implementare il multi-threading nel backtest di strategie di trading in Python su coppie di titoli azionari co-integrati. Per il codice completo riportato in questo articolo, si può consultare il seguente repository di github:
https://github.com/datatrading-info/Backtest_Strategie





