In questo articolo descriviamo come implementare una logica mean-reverting con python da usare per il backtest di una strategia mean-reverting di trading algoritmico. L’articolo fa parte della miniserie “Backtest di una strategia di mean reverting con gli ETF”.
Gli articoli che fanno parte di questa serie sono:
- Backtest ETF: Web scraping e Database Sqlite3
- Backtest ETF: Creazione di coppie di Ticker
- Backtest ETF: Mean-reverting con Python
- Backtest ETF: Strategia di Trading con lo Z-score
- Backtest ETF: Pair trading con Python
L’articolo descrive le fasi iniziali di implementazione di una logica di ritorno alla media con Python per il backtesting della strategia. Non usiamo la funzione di “coppie di simboli” che abbiamo creato nel precedente articolo ma ci concentriamo su una singola coppia di simboli per eseguire le prime fasi del backtest in modo da poter velocemente effettuare le prime verifiche.
Dopo aver verificato che lo script funziona per una singola una coppia di simboli, possiamo molto facilmente estenderlo per lavorare con la lista di coppie di simboli creata in precedenza.
La logica
In particolare, in questo articolo approfondiamo quanto segue:
- Definire la coppia di simboli, scaricare i relativi dati storici da yahoo Finance e assicurarsi che i dati scaricati per ogni simbolo siano della stessa lunghezza.
- Visualizzare le due serie di prezzi degli ETF, l’una contro l’altra, per ottenere una rappresentazione visiva e quindi eseguire un “jointplot” di Seaborn per analizzare la forza della correlazione tra le due serie.
- Eseguire una regressione dei minimi quadrati ordinari sui prezzi di chiusura per calcolare un rapporto di copertura. Usare il rapporto di copertura per generare e visualizzare lo spread tra i due prezzi per verificare se sembra mean-reverting.
- Eseguire un test Augmented Dickey Fuller sullo spread per confermare statisticamente se la serie è mean-reverting o meno. Calcolare anche l’esponente di Hurst della serie dello spread.
- Eseguire una regressione dei minimi quadrati ordinari sulla serie spread e una versione ritardata della serie spread per poi usare il coefficiente per calcolare il mean-reverting.
Il codice
Adesso passiamo al codice… Iniziamo con importare i moduli pertinenti di cui abbiamo bisogno, definire i simboli dei ticker ETF e scaricare i dati dei prezzi da Yahoo Finance.
from datetime import datetime
import pandas as pd
import numpy as np
from numpy import log, polyfit, sqrt, std, subtract
import statsmodels.tsa.stattools as ts
import statsmodels.api as sm
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_style('whitegrid')
import pprint
import yfinance as yf
# Scegliere la coppia di ticker per il testing
symbList = ['EWA', 'EWC']
start_date = '2012-01-01'
end_date = '2020-01-01'
# Download i dati da Yahoo Finance
y=yf.download(symbList[0], start=start_date, end=end_date)
x=yf.download(symbList[1], start=start_date, end=end_date)
# Rinomina le colonne
y.rename(columns={'Adj Close':'price'}, inplace=True)
x.rename(columns={'Adj Close':'price'}, inplace=True)
# Verificare che i dataframe sono della stessa lunghezza
min_date = max(df.dropna().index[0] for df in [y, x])
max_date = min(df.dropna().index[-1] for df in [y, x])
y = y[(y.index>= min_date) & (y.index <= max_date)]
x = x[(x.index >= min_date) & (x.index <= max_date)]
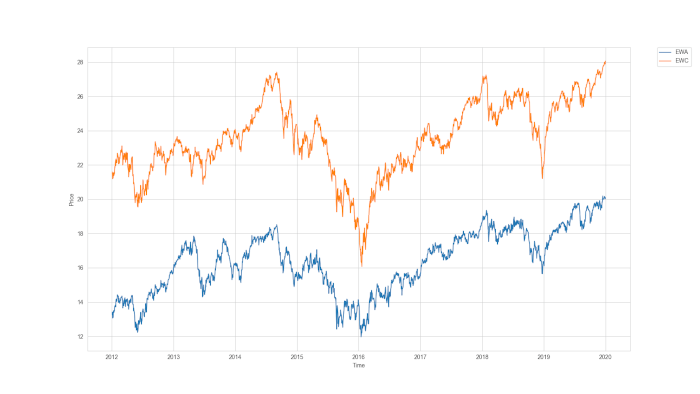
Dopo avere ottenuto i dati sui prezzi archiviati in un DataFrames, visualizziamo una grafico delle due serie per individuare quali informazioni possiamo raccogliere.
# Grafico delle serie
plt.plot(y.price,label=symbList[0])
plt.plot(x.price,label=symbList[1])
plt.ylabel('Price')
plt.xlabel('Time')
plt.legend(bbox_to_anchor=(1.05, 1), loc=2, borderaxespad=0.)
plt.show()
jointplot di Seaborn come segue:
sns.jointplot(y.price, x.price ,color='b')
plt.show()
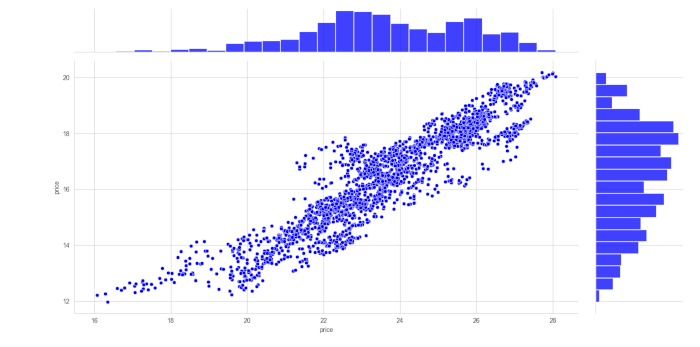
Dalle informazioni fornite nel grafico possiamo vedere che il coefficiente di correlazione di Pearson è pari a 0,87, quindi abbiamo sicuramente una correlazione piuttosto forte tra le serie di prezzi. La coppia è quindi potenzialmente adatta per una strategia di ritorno alla media.
# esegue la regressione dei minimi quadrati ordinari per trovare
# il rapporto di copertura e quindi creare serie di spread
df1 = pd.DataFrame({'y':y['price'],'x':x['price']})
est = sm.OLS(df1.y,df1.x)
est = est.fit()
df1['hr'] = -est.params[0]
df1['spread'] = df1.y + (df1.x * df1.hr)
Tramite la regressione tra le serie di prezzi dell’ETF abbiamo ricavato il coefficiente beta che è stato poi usato come rapporto di copertura per creare la serie di spread dei due prezzi.
Se visualizziamo la serie di spread otteniamo il seguente grafico:
plt.plot(df1.spread)
plt.show()

Il grafico sembra relativamente mean-reverting ma, a volte, l’aspetto può ingannare. Per avere un’idea migliore, dobbiamo effettuare alcune verifiche tramite test statistici sulle serie diffuse. Usiamo il Dickey-Fuller Aumentato (ADF). Per approfondire le basi di questo test è possibile leggere l’articolo sul Testing Statistico della Mean Reversion.
cadf = ts.adfuller(df1.spread)
print('Augmented Dickey Fuller test statistic =', cadf[0])
print('Augmented Dickey Fuller p-value =', cadf[1])
print('Augmented Dickey Fuller 1%, 5% and 10% test statistics =', cadf[4])
Otteniamo il seguente risultato:
Augmented Dickey Fuller test statistic = -4.027995814086793
Augmented Dickey Fuller p-value = 0.0012708069697384807
Augmented Dickey Fuller 1%, 5% and 10% test statistics = {'1%': -3.4336075477138945, '5%': -2.862979013123536, '10%': -2.567536068414148}
Vediamo che la statistica del test è pari a -4,028, maggiore in termini assoluti della statistica test del 10% di -2,567, della statistica test del 5% di -2,863 e della statistica test dell’1% di -3,433. Possiamo quindi rifiutare l’ipotesi nulla che esista una radice unitaria nella serie dello spread, e quindi la serie è mean-reverting per i livelli di significatività del 10%, del 5% e dell’1%.
Inoltre Il p-value pari a 0,0191 significa che possiamo rifiutare l’ipotesi nulla fino al livello di significatività dell’1,91%. Questo è abbastanza buono in termini di significatività statistica, e da questo possiamo essere abbastanza certi che la serie dello spred è effettivamente mean-reverting.
Come ulteriore verifica eseguiamo una semplice funzione per calcolare l’esponente di Hurst della serie di spread. Per informazioni sull’esponente di Hurst si può leggere l’articolo sul Testing Statistico della Mean Reversion.
Per semplificare i concetti, dobbiamo semplicemente ricordarci che l’esponente di Hurst (H) caratterizza una serie temporale nel modo seguente:
- H < 0.5 – La serie temporale è un mean reverting
- H = 0.5 – La serie temporale è un moto browniano geometrico
- H > 0.5 – La serie temporale è in tendenza
ed ecco il codice:
def hurst(ts):
"""
Restituisce l'Esponente Hurst Exponent del vettore della serie temporale ts
"""
# Crea il range dei valori ritardati
lags = range(2, 100)
# Calcola l'array delle variance delle differenze dei ritardi
tau = [sqrt(std(subtract(ts[lag:], ts[:-lag]))) for lag in lags]
# Usa una regressione lineare per stimare l'Esponente di Hurst
poly = polyfit(log(lags), log(tau), 1)
# Restituisce l'Esponente di Hurst dall'output di polyfit
return poly[0] * 2.0
Ora eseguiamo la funzione sulla serie di spread:
print("Hurst Exponent =",round(hurst(df1.spread.to_list()),2))
E otteniamo:
Hurst Exponent = 0.4
L’esponente di Hurst è al di sotto del valore 0,5 (corrispondente ad una passeggiata casuale) e quindi possiamo concludere che la serie è mean-reverting, confermando la conclusione basata sul precedente test di Dickey Fuller Aumentato. La serie degli spread sembra quindi un candidato ideale per una strategia di mean-reverting dato che mostra proprietà di ritorno alla media.
Tuttavia, solo perché una serie temporale mostra proprietà di ritorno alla media, non significa necessariamente che possiamo applicare con profitto una strategia mean-reverting: c’è una differenza tra una serie che si allontana e ritorna verso la media ogni settimana e una che impiega 10 anni per ritornare ai valori medi. Non sono sicuro che molti trader sarebbero disposti ad aspettare per 10 anni per chiudere un’operazione con profitto.
Per avere un’idea di quanto tempo impiega ogni serie a tornare al valore medio possiamo esaminare la “Emivita” delle serie temporali. Per ulteriori informazioni sull’emivita si può consultare questo link. Possiamo calcolarlo eseguendo una regressione lineare tra la serie di spread e una versione ritardata di se stessa. Il coefficiente Beta prodotto da questa regressione può quindi essere incorporato nel processo di Ornstein-Uhlenbeck per calcolare l’emivita. Per approfondire il processo di Ornstein-Uhlenbeck si può leggere questo articolo.
Il codice per calcolarlo è il seguente:
# Calcolo della regressione OLS per la serie degli spread e la sua versione ritardata
spread_lag = df1.spread.shift(1)
spread_lag.iloc[0] = spread_lag.iloc[1]
spread_ret = df1.spread - spread_lag
spread_ret.iloc[0] = spread_ret.iloc[1]
spread_lag2 = sm.add_constant(spread_lag)
model = sm.OLS(spread_ret,spread_lag2)
res = model.fit()
halflife = round(-np.log(2) / res.params[1],0)
print('Halflife = ',halflife)
E otteniamo:
Halflife = 42.0
Vediamo come l’emivita del ritorno alla media è pari a 42 giorni. Non è poi così male, e non tanto da escluderlo automaticamente come candidato per una strategia di mean reversion. Idealmente l’emivita dovrebbe essere la più breve possibile in modo da fornirci opportunità di trading più redditizie, ma in questo caso dobbiamo accontentarci di 42 giorni.
Nel prossimo articolo descriviamo come ottenere una serie normalizzata di “Z-score” per poter misurare l’allontanamento dalla media locale in termini di deviazioni standard. Vediamo poi come effettuare il backtest usando Pandas e se possiamo ottenere qualcosa di redditizio.




