DATATRADER

Introduzione all’Ottimizzazione di una Strategia – Parte II

Scritto da
Gianluca

Il precedente articolo si è concentrato sulla selezione del modello e sull’ottimizzazione del modello statistico sottostante che (potrebbe) costituire la base di una strategia di trading. Tuttavia, un modello predittivo e una strategia algoritmica funzionante e redditizia sono due entità diverse. Questo articolo rivolge l’attenzione all’ottimizzazione dei parametri che hanno un effetto diretto sulla redditività e sulle metriche del rischio.
Per raggiungere questo obiettivo si utilizza un software di backtesting event-driven, come descritto in un questa serie di articoli. Si prende inoltre in considerazione una particolare strategia che ha tre parametri ad essa associati, e si effettua uno studio sullo spazio formato dal prodotto cartesiano dei parametri, utilizzando il metodo della grid search. Quindi si tenta di massimizzare alcune specifiche metriche, come il Sharpe Ratio, o minimizzarne altre, come il drawdown massimo.

Strategia Intraday di Pairs Trading sull'azionario

La strategia che si prende in considerazione è la “Intraday Mean Reverting Equity Pairs Trade” utilizzando le AREX e WLL del settore energetico, come descritto in un precedente articolo. Questa strategia prevede tre parametri che si possono ottimizzare: il periodo di ricerca della regressione lineare, i residui delle soglie di z-score di entrata e i residui delle soglie di z-score di uscita.
Si considera un intervallo di valori per ogni parametro e quindi si effettua il backtesting della strategia per ciascuno di questi intervalli, ricavando il rendimento totale, il Sharpe Ratio e le caratteristiche di drawdown per ogni simulazione, e memorizza i risultati in un file CSV per ogni set di parametri. Questo permette di ricavare uno Sharpe ottimizzato o un drawdown massimo minimizzato per la strategia di trading oggetto di analisi.,

Aggiustamento dei Parametri

Dato che il software di backtesting basato sugli eventi è piuttosto oneroso per il carico di lavoro sulla CPU, si limita l’intervallo di parametri a solo tre valori per ogni parametro. Questo fornisce un totale di \( 3^{3} = 27\) separate simulazioni da eseguire. Gli intervalli dei parametri sono elencati di seguito:

OLS Lookback Window – \( w_i \in \big\{50, 100, 200\big\}\)
Z-Score Entry Threshold – \( z_h \in \big\{2.0, 3.0, 4.0\big\}\)
Z-Score Exit Threshold – \( z_l \in \big\{0.5, 1.0, 1.5\big\}\)

Per eseguire l’insieme di simulazioni si calcola un prodotto cartesiano di tutte e tre gli intervalli e si esegue la simulazione per ciascuna combinazione di parametri (ciascun prodotto cartesiano). Il primo passo è modificare il file intraday_mr.py ed includere il metodo product dalla libreria itertools:

            # intraday_mr.py
..
from itertools import product
..

E’ quindi necessario modificare il metodo principale __main__ per includere la generazione di un elenco di valori per tutti e tre i parametri, descritti in precedenza. Il primo passo consiste nel creare gli effettivi intervalli dei parametri per la finestra di ricerca OLS, la soglia di ingresso dello zscore e la soglia di uscita dello zscore. Ognuno di questi può assumere 3 diversi valori quindi la loro combinazione causa un totale di 27 simulazioni.

Una volta creati gli intervalli, si usa il metodo itertools.product per creare un prodotto cartesiano di tutti i valori, che sono poi inseriti all’interno di un dizionario al fine di garantire che i corretti argomenti siano passati all’oggetto Strategy. Infine, il backtest viene istanziato con la strat_params_list che contiene il dizionario di tutte le combinazioni dei parametri:

            
if __name__ == "__main__":
   csv_dir = ’/path/to/your/csv/file’ # CHANGE THIS!
   symbol_list = [’AREX’, ’WLL’]
   initial_capital = 100000.0
   heartbeat = 0.0
   start_date = datetime.datetime(2007, 11, 8, 10, 41, 0)

   # Create the strategy parameter grid
   # using the itertools cartesian product generator
   strat_lookback = [50, 100, 200]
   strat_z_entry = [2.0, 3.0, 4.0]
   strat_z_exit = [0.5, 1.0, 1.5]
   strat_params_list = list(product(
         strat_lookback, strat_z_entry, strat_z_exit
        ))

   # Create a list of dictionaries with the correct
   # keyword/value pairs for the strategy parameters
   strat_params_dict_list = [
        dict(ols_window=sp[0], zscore_high=sp[1], zscore_low=sp[2])
        for sp in strat_params_list
       ]

    # Carry out the set of backtests for all parameter combinations
    backtest = Backtest(
           csv_dir, symbol_list, initial_capital, heartbeat,
           start_date, HistoricCSVDataHandlerHFT, SimulatedExecutionHandler,
           PortfolioHFT, IntradayOLSMRStrategy,
           strat_params_list=strat_params_dict_list
        )
    backtest.simulate_trading()

Il passaggio successivo consiste nel modificare l’oggetto Backtest in backtest.py per poter gestire più set di parametri. In particolare si modifica il metodo _generate_trading_instances per avere un argomento che rappresenti lo specifico parametro impostato sulla creazione di un nuovo oggetto Strategy:

            # backtest.py
..

def _generate_trading_instances(self, strategy_params_dict):
    """
    Generates the trading instance objects from
    their class types.
    """
    print("Creating DataHandler, Strategy, Portfolio and ExecutionHandler for")
    print("strategy parameter list: %s..." % strategy_params_dict)
    self.data_handler = self.data_handler_cls(
        self.events, self.csv_dir, self.symbol_list, self.header_strings
        )
    self.strategy =    
    self.strategy_cls(
        self.data_handler, self.events, **strategy_params_dict
        )
    self.portfolio = self.portfolio_cls(
        self.data_handler, self.events, self.start_date,
        self.num_strats, self.periods, self.initial_capital
        )
    self.execution_handler = self.execution_handler_cls(self.events)

Questo metodo è richiamato all’interno di un ciclo iterativo della lista dei parametri della strategia, invece che in fase di costruzione dell’oggetto Backtest. Nonostante ricreare tutti i gestori di dati, la coda degli ‘eventi e oggetti portfolio per ogni set di parametri possa sembrare uno spreco, questo assicura che tutte le variabili siano state resettate ad ogni iterazione e quindi avere un “ambiente pulito” per ogni simulazione.

Il prossimo passo consiste nel modificare il metodo simulate_trading per eseguire il loop su tutte le possibili combinazioni dei parametri della strategia. Il metodo crea un file CSV di output che viene utilizzato per memorizzare le combinazioni di parametri e le loro specifiche metriche di performance. Questo consente di tracciare l’andamento delle prestazioni tra i parametri.

Il metodo effettua un loop su tutti i parametri della strategia e genera una nuova istanza di trading su ogni simulazione. Si esegue quindi il backtesting e si calcolano le statistiche. Questi dati sono raccolti in un file CSV. Al termine della simulazione, il file di output viene chiuso e memorizzato:

            # backtest.py

..
def simulate_trading(self):
    """
    Simulates the backtest and outputs portfolio performance.
    """
    out = open("output/opt.csv", "w")
    spl = len(self.strat_params_list)
    for i, sp in enumerate(self.strat_params_list):
        print("Strategy %s out of %s..." % (i+1, spl))
        self._generate_trading_instances(sp)
        self._run_backtest()
        stats = self._output_performance()
        pprint.pprint(stats)
        tot_ret = float(stats[0][1].replace("%",""))
        cagr = float(stats[1][1].replace("%",""))
        sharpe = float(stats[2][1])
        max_dd = float(stats[3][1].replace("%",""))
        dd_dur = int(stats[4][1])
        out.write(
            "%s,%s,%s,%s,%s,%s,%s,%s\n" % (
                sp["ols_window"], sp["zscore_high"], sp["zscore_low"],
                tot_ret, cagr, sharpe, max_dd, dd_dur
                )
        )
        out.close()

Su un normale sistema desktop, questo processo richiede del tempo! Per 27 simulazioni su oltre 600.000 punti dati per simulazione sono state necessarie almeno 2 ore. In questa fase backtester non è stato parallelizzato, quindi la contemporanea esecuzione di più simulazioni in parallelo renderebbe il processo molto più veloce. L’output per l’attuale spazio dei parametri corrente è riportato di seguito. Le colonne corrispondo a OlS Lookback, ZScore High, ZScore Low, Total Return (%), CAGR (%), Sharpe, Max DD (%), DD Duration (minuti):

            50,2.0,0.5,213.96,20.19,1.63,42.55,255568
50,2.0,1.0,264.9,23.13,2.18,27.83,160319
50,2.0,1.5,167.71,17.15,1.63,60.52,293207
50,3.0,0.5,298.64,24.9,2.82,14.06,35127
50,3.0,1.0,324.0,26.14,3.61,9.81,33533
50,3.0,1.5,294.91,24.71,3.71,8.04,31231
50,4.0,0.5,212.46,20.1,2.93,8.49,23920
50,4.0,1.0,222.94,20.74,3.5,8.21,28167
50,4.0,1.5,215.08,20.26,3.66,8.25,22462
100,2.0,0.5,378.56,28.62,2.54,22.72,74027
100,2.0,1.0,374.23,28.43,3.0,15.71,89118
100,2.0,1.5,317.53,25.83,2.93,14.56,80624
100,3.0,0.5,320.1,25.95,3.06,13.35,66012
100,3.0,1.0,307.18,25.32,3.2,11.57,32185
100,3.0,1.5,306.13,25.27,3.52,7.63,33930
100,4.0,0.5,231.48,21.25,2.82,7.44,29160
100,4.0,1.0,227.54,21.01,3.11,7.7,15400
100,4.0,1.5,224.43,20.83,3.33,7.73,18584
200,2.0,0.5,461.5,31.97,2.98,19.25,31024
200,2.0,1.0,461.99,31.99,3.64,10.53,64793
200,2.0,1.5,399.75,29.52,3.57,10.74,33463
200,3.0,0.5,333.36,26.58,3.07,19.24,56569
200,3.0,1.0,325.96,26.23,3.29,10.78,35045
200,3.0,1.5,284.12,24.15,3.21,9.87,34294
200,4.0,0.5,245.61,22.06,2.9,12.52,51143
200,4.0,1.0,223.63,20.78,2.93,9.61,40075
200,4.0,1.5,203.6,19.55,2.96,7.16,40078

Da notare che per la particolare combinazione dei parametri pari a w_l = 50, z_h = 3.0 e z_l = 1.5 si ha il miglior Sharpe Ratio, pari a S = 3.71. Per questo Sharpe Ratio si ha un total return del 294.91% e drawdown massimo del 8.04%. Il migliore total return è del 461.99%, a cui corrisponde pero un drawdown massimo del 10.53%, si verifica per il set di parametri con w_l = 200, z_h = 2.0 e z_l = 1.0.

Visualizzazione

Come passo finale nell’ottimizzazione di una strategia, si può visualizzare le prestazioni del backtesting usando Matplotlib, che può essere estramemente utile quando si effettuano le iniziali studi su una strategia. Purtroppo lo scenario preso in considerazione ha uno spazio delle soluzioni tridimensionale quindi la visualizzazione delle prestazioni non è immediata! Tuttavia, si possono fare alcuni miglioramenti. In primo luogo, si può fissare il valore di un parametro e prendere una “sezione parametri” attraverso il resto del “cubo di dati”. Ad esempio, si può fissare la finestra di ricerca a 100 e poi vedere come la variazione delle soglie di entrata e di uscita dello z-score influenza il Sharpe Ratio o il drawdown massimo. Per raggiungere questo obiettivo si utilizza Matplotlib. Si acquisisce l’output CSV e si rimodella i dati in modo tale che si possa visualizzare i risultati.

Heatmap del Ratio / Drawdown

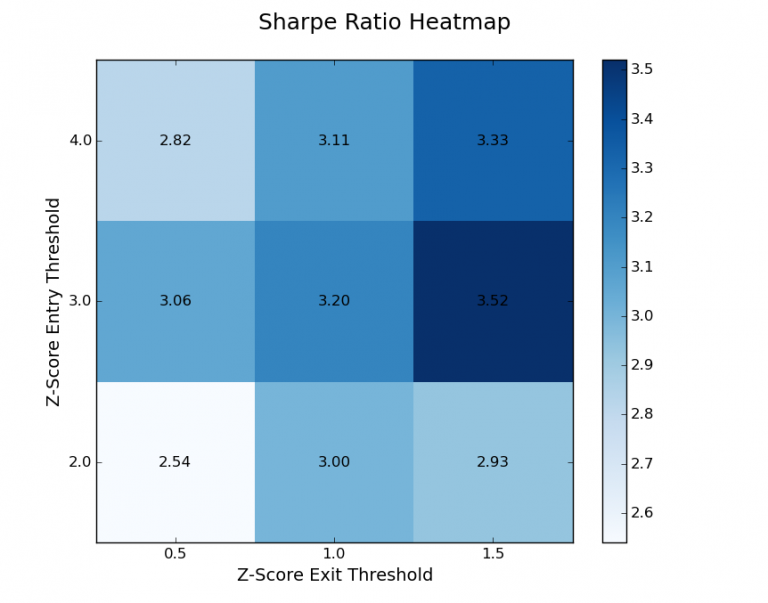
Fissato il periodo di ricerca a w_l = 100 si genera una griglia 3×3 e una “heatmap” del Sharpe Ratio e drawdown massimo per la variazione delle soglie z-score.
Nel seguente codice si acquisisce il file CSV di output. Il primo compito è filtrare i periodi di ricerca che ci interessano (50 e 200). Quindi si modifica i restanti dati sulle prestazioni in due matrici 3×3. Il primo rappresenta il Sharpe Ratio per ogni combinazione delle soglie dello z-score mentre il secondo rappresenta il drawdown massimo.

Ecco il codice per creare la heatmap dello Sharpe Ratio. Per prima cosa si importa Matplotlib e NumPy. Quindi si definisce una funzione chiamata create_data_matrix che rimodella i dati dello Sharpe Ratio in una griglia 3×3. All’interno della funzione principale __main__ si apre il file CSV (assicurarsi di cambiare il percorso sul file system del sistema!) E si esclude qualsiasi record che non faccia riferimento a un periodo di ricerca di 100.
Si crea quindi una heatmap con ombreggiatura blu e si applicano le corrette etichette di riga / colonna usando le soglie dello z-score. Successivamente si posiziona il valore effettivo del Sharpe Ratio sulla heatmap. Infine, si imposta tick, etichette, titolo e quindi si traccia la heatmap:

            #!/usr/bin/python
# -*- coding: utf-8 -*-

# plot_sharpe.py

import matplotlib.pyplot as plt
import numpy as np

def create_data_matrix(csv_ref, col_index):
    data = np.zeros((3, 3))
    for i in range(0, 3):
        for j in range(0, 3):
            data[i][j] = float(csv_ref[i*3+j][col_index])
            return data


if __name__ == "__main__":
    # Open the CSV file and obtain only the lines
    # with a lookback value of 100
    csv_file = open("/path/to/opt.csv", "r").readlines()
    csv_ref = [
        c.strip().split(",")
        for c in csv_file if c[:3] == "100"
        ]
    data = create_data_matrix(csv_ref, 5)

    fig, ax = plt.subplots()
    heatmap = ax.pcolor(data, cmap=plt.cm.Blues)
    row_labels = [0.5, 1.0, 1.5]
    column_labels = [2.0, 3.0, 4.0]
    for y in range(data.shape[0]):
        for x in range(data.shape[1]):
            plt.text(x + 0.5, y + 0.5, ’%.2f’ % data[y, x],
                horizontalalignment=’center’,
                verticalalignment=’center’,
            )
    plt.colorbar(heatmap)

    ax.set_xticks(np.arange(data.shape[0])+0.5, minor=False)
    ax.set_yticks(np.arange(data.shape[1])+0.5, minor=False)
    ax.set_xticklabels(row_labels, minor=False)
    ax.set_yticklabels(column_labels, minor=False)

    plt.suptitle(’Sharpe Ratio Heatmap’, fontsize=18)
    plt.xlabel(’Z-Score Exit Threshold’, fontsize=14)
    plt.ylabel(’Z-Score Entry Threshold’, fontsize=14)
    plt.show()

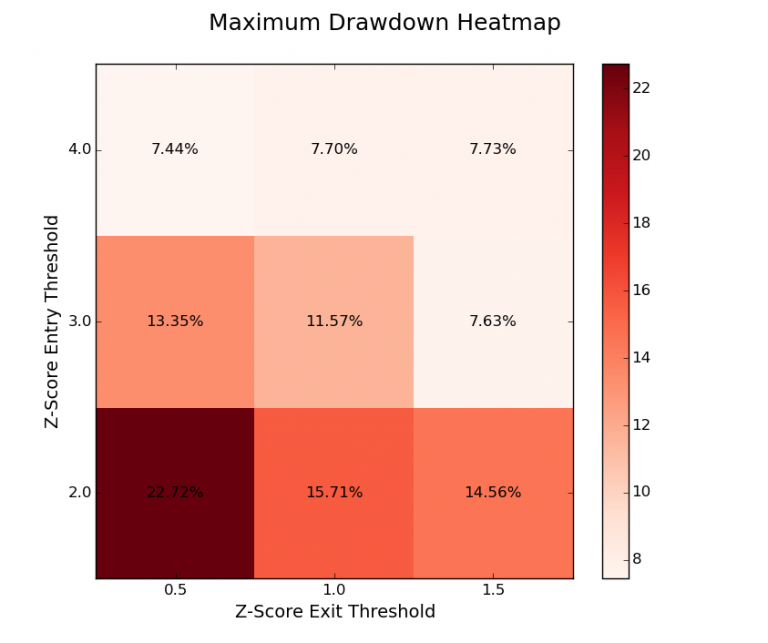
Il grafico del drawdown massimo è quasi identica ad eccezione dell’utilizzo di una heatmap con ombreggiatura rossa e la modifica dell’indice di colonna nella funzione create_data_matrix per usare i dati percentuali del drawdown massimo.

            #!/usr/bin/python
# -*- coding: utf-8 -*-

# plot_drawdown.py

import matplotlib.pyplot as plt
import numpy as np

def create_data_matrix(csv_ref, col_index):
    data = np.zeros((3, 3))
    for i in range(0, 3):
        for j in range(0, 3):
            data[i][j] = float(csv_ref[i*3+j][col_index])
            return data


if __name__ == "__main__":
    # Open the CSV file and obtain only the lines
    # with a lookback value of 100
    csv_file = open("/path/to/opt.csv", "r").readlines()
    csv_ref = [
        c.strip().split(",")
        for c in csv_file if c[:3] == "100"
        ]
    data = create_data_matrix(csv_ref, 6)

    fig, ax = plt.subplots()
    heatmap = ax.pcolor(data, cmap=plt.cm.Reds)
    row_labels = [0.5, 1.0, 1.5]
    column_labels = [2.0, 3.0, 4.0]
    for y in range(data.shape[0]):
        for x in range(data.shape[1]):
            plt.text(x + 0.5, y + 0.5, ’%.2f’ % data[y, x],
                horizontalalignment=’center’,
                verticalalignment=’center’,
            )
    plt.colorbar(heatmap)

    ax.set_xticks(np.arange(data.shape[0])+0.5, minor=False)
    ax.set_yticks(np.arange(data.shape[1])+0.5, minor=False)
    ax.set_xticklabels(row_labels, minor=False)
    ax.set_yticklabels(column_labels, minor=False)

    plt.suptitle(’Drawdown Heatmap’, fontsize=18)
    plt.xlabel(’Z-Score Exit Threshold’, fontsize=14)
    plt.ylabel(’Z-Score Entry Threshold’, fontsize=14)
    plt.show()

I grafici delle Heatmap per lo Sharpe Ratio e il Drawdown Massimo sono riportati di seguito

Con w_l = 100 le differenze tra il più piccolo e il più grande Sharpe Ratio più piccolo e il più grande, così come tra il più piccolo e il più grande drawdown massimo, sono molto evidenti. Il Sharpe Ratio è ottimizzato per le soglie di entrata e uscita più grandi, mentre il drawdown è ridotto al minimo nella stessa regione. Il Sharpe Ratio e il drawdown massimo sono peggiori quando entrambe le soglie di ingresso e di uscita sono basse.