In questo articolo esaminiamo e confrontiamo i concetti dell’analisi Monte Carlo e Bootstrapping con Python, per simulare una serie di rendimenti e generare gli intervalli di confidenza corrispondenti ai potenziali rischi e benefici di un portafoglio di investimento. Per approfondire si può consultare il precedente articolo sulle simulazione Monte Carlo con Python.
Entrambi i metodi sono usati per generare andamenti simulati di serie di prezzi per un determinato asset o portafoglio di asset. Questi metodi si basano su approcci leggermente diversi, che possono sembrare trascurabile per coloro che non hanno un background matematico. Tecnicamente il bootstrap è un caso particolare della simulazione Monte Carlo, quindi a prima vista può sembrare uguale.
La teoria
Con l’analisi Monte Carlo (in particolare ci riferiamo specificamente dell’approccio Monte Carlo “Parametrico”) l’idea è quella di generare dati basati su alcune caratteristiche del modello sottostante. Quindi, ad esempio, generiamo dati basati su una distribuzione normale, specificando i parametri desiderati per il modello. In questo caso la media e la deviazione standard. Questi valori sono generalmente calcolati dai valori storici e realizzati per gli asset che si vuole analizzare.
Se proviamo ad effettuare alcune simulazioni Monte Carlo parametriche per generare dati simulati di un titolo azionario tendiamo a misurare e calcolare la media e la deviazione standard degli effettivi rendimenti storici delle azioni per un periodo di tempo e usarle come input per il modello. Questo è uno dei punti deboli di questo approccio, perchè l’output del modello e le relative inferenze dipendono da rendimenti futuri che mostreranno le stesse caratteristiche dei rendimenti storici (di quelli usati per calcolare gli input del modello).
In cosa consiste il bootstrapping e in cosa si differenza dal Monte Carlo? Anche il bootstrapping usa i rendimenti storici come input del modello, ma sono usati in modo più esplicito. Nel bootstrapping usiamo i rendimenti storici per generare i dati campionati, invece di calcolare le caratteristiche sottostanti e quindi inserirle in un modello parametrico.
Da sottolineare che il bootstrapping implica la “sostituzione” e quindi rientra nella famiglia dei metodi di “campionamento con sostituzione”. Questo metodo prevede che quando un campione casuale è estratto dalla distribuzione dei rendimenti storici, non è “buttato via” e rimosso dall’insieme, ma è sostituito e rimesso nell’insieme. Può quindi essere scelto nuovamente durante le successive estrazioni campionarie.
Questo approccio si traduce in un risultato fondamentalmente diverso da quello che ottiene dal “campionamento senza sostituzione”, dove ogni dato è rimosso dal campione dopo essere stato “estratto”.
Come detto, la logica alla base del metodo Bootstrapping prevede di usare il campionamento con sostituzione. Questo significa che ogni campione estratto, se casuale, ha la stessa possibilità di verificarsi che avrebbe nella “vita reale”, cioè la probabilità che avrebbe nei mercati reali per quello specifico titolo azionario. Da notare che anche questo approccio si basa sull’ipotesi che la distribuzione dei rendimenti futuri avrà le stesse caratteristiche della distribuzione dei rendimenti storici da cui sono estratti i campioni. In altre parole sia le distribuzioni dei rendimenti futuri che quelle passate sono tratte dalla stessa “popolazione”.
Definizione del portafoglio di asset
Per capire e verificare questi concetti, consideriamo i dati storici di un paniere di titoli e creiamo un portafoglio equi-pesato. Eseguiamo quindi le simulazioni Monte Carlo e il Bootstrapping e confrontiamo i due risultati per verificare le differenze. Iniziamo importando i moduli e configurando alcune variabili.
import pandas as pd
import numpy as np
from functools import reduce
import yfinance as yf
import datetime
import random
import matplotlib.pyplot as plt
import matplotlib as mpl
import seaborn as sns
mpl.style.use('ggplot')
figsize = (15, 8)
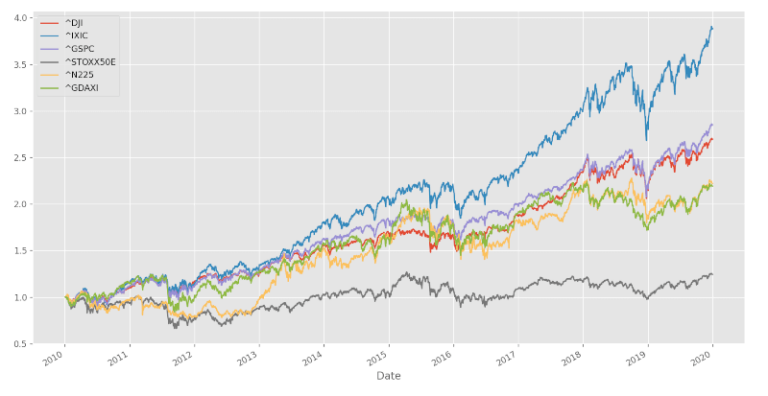
Scarichiamo i dati storici dei prezzi da Yahoo per alcuni indici azionari tramite la libreria yfinance e li normalizziamo in modo che tutti inizino da 1 per facilitare il confronto.
start, end = '2010-01-01', '2020-01-01'
tickers = ["^DJI", "^IXIC", "^GSPC", "^STOXX50E", "^N225", "^GDAXI"]
asset_universe = pd.DataFrame([yf.download(ticker, start, end).loc[:, 'Adj Close'] for ticker in tickers], index=tickers)
asset_universe = asset_universe.T.fillna(method='ffill')
asset_universe = asset_universe/asset_universe.iloc[0, :]
Tracciamo il grafico delle serie dei prezzi degli asset scaricati.
asset_universe.plot(figsize=figsize)
Quando eseguiamo il Bootstrapping su un portafoglio di asset, è di vitale importanza assicurarsi di procedere correttamente. L’approccio deve considerare eventuali correlazioni tra gli asset. Se non lo facciamo otteniamo risultati che si discostano dalla realtà.
Prendiamo ad esempio due azioni che sono molto correlate negativamente e prevediamo di campionare indipendentemente ogni azione. Quando effettuiamo un’estrazione casuale, potremmo estrarre un campione per l’azione 1 che si è verificato in un giorno particolare ed estrarre un campione per per l’azione 2 che si è verificata in un giorno diverso, Se vediamo che i campioni per l’azione 1 e l’azione 2 sono stati molto positivi, possiamo davvero considerare che sia un campione veramente rappresentativo della reale relazione tra le azioni?
La risposta è no, perché stiamo confrontando “mele con pere”. E’ fondamentale che i campioni per i componenti del portafoglio siano estratti nello stesso periodo di tempo. Solo in questo caso le correlazioni intrinseche tra tutti gli asset saranno correttamente catturate dai campioni casuali.
Possiamo quindi procedere generando più estrazioni casuali (con sostituzione) da tutte le singole serie di rendimenti storici che costituiscono il portafoglio. Possiamo quindi pesarle di conseguenza, e infine sommare i rendimenti pesati e memorizzare il risultato corrispondente come il “rendimento di portafoglio” di Bootstrapping. Dobbiamo ripetere questa procedura molte volte, memorizzando ogni volta il “rendimento del portafoglio” simulato. L’insieme delle serie di rendimenti simulati corrisponde al risultato del Bootstrapping.
In alternativa, possiamo costruire il rendimento del portafoglio pesando i costituendi dei rendimenti storici, sommandoli e quindi applicare il processo di bootstrapping a quella singola distribuzione del rendimento storico del portafoglio. I risultati sono praticamente analoghi dato che il portafoglio è stato costruito in modo da conservare intrinsecamente l’effetto di eventuali correlazioni tra gli asset che compongono il portafoglio. In altre parole la serie dei rendimenti è stata calcolata usando i rendimenti pesati degli asset costitutivi, verificatesi nello stesso giorno. Quindi possiamo semplicemente eseguire il Bootstrapping del singolo portafoglio, generando nuovamente più andamenti dei rendimenti simulati e l’insieme degli andamenti il risutato del Bootstrapping.
Iniziamo con il secondo approccio e creiamo la nostra serie di rendimenti di portafoglio ugualmente pesato. Prendiamo solo la media dei singoli rendimenti costitutivi per un portafoglio equi-pesato. Tracciamo quindi la “serie dei prezzi” del portafoglio rispetto ai singoli componenti.
portfolio_returns = asset_universe.pct_change().dropna().mean(axis=1)
portfolio = (asset_universe.pct_change().dropna().mean(axis=1) + 1).cumprod()
asset_universe.plot(figsize=figsize, alpha=0.4)
portfolio.plot(label='Portfolio', color='black')
plt.legend()
plt.show()
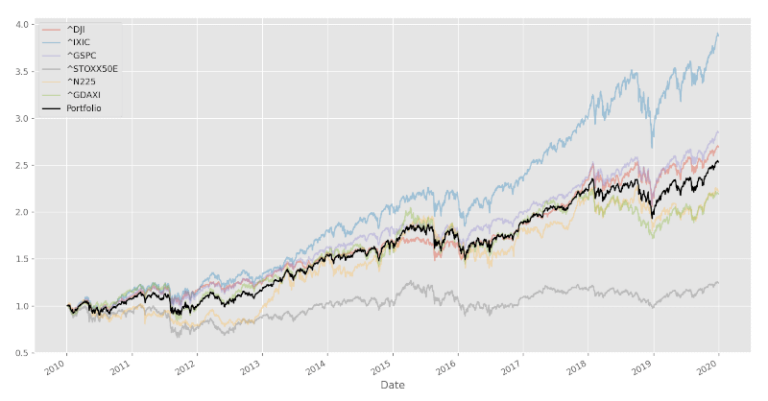
Vediamo che i rendimenti del portafoglio sono nel mezzo dei rendimenti dei singoli indici. Infatti, dato che il portafoglio è equi-pesato, per costruzione finisce esattamente nel “mezzo” dei rendimenti degli asset costitutivi.
Analisi del Bootstrapping
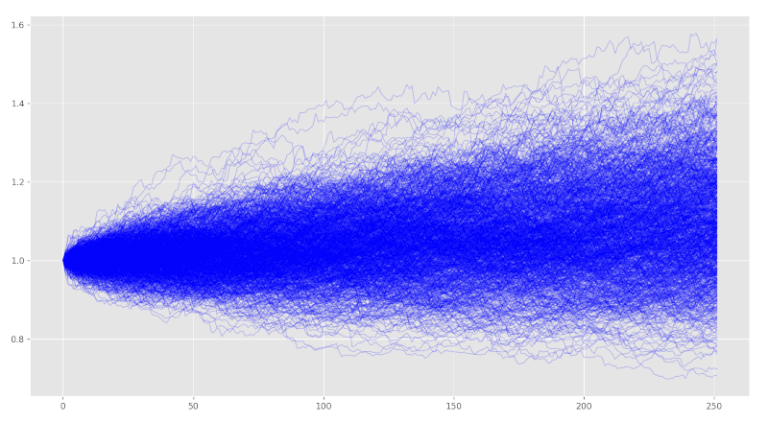
Eseguiamo ora il processo Bootstrapping sulla serie dei rendimenti del portafoglio e tracciamo i risultati.
portfolio_bootstrapping = pd.DataFrame([random.choices(list(portfolio_returns.values), k=252) for i in range(1000)])
portfolio_bootstrapping = (1+portfolio_bootstrapping.T.shift(1).fillna(0)).cumprod()
portfolio_bootstrapping.plot(figsize=figsize, legend=False, linewidth=1, alpha=0.2, color='b')
plt.show()
Vediamo ora come l’approccio opposto produce gli stessi risultati. Prendiamo campioni delle singole serie di rendimenti degli asset e li usiamo per creare le simulazioni di Bootstrapping. Otteniamo lo stesso risultato a meno di un un elemento casuale che rende ogni simulazione diversa anche se basata sullo stesso approccio. Di seguito è riportato il codice che lo implementa,
asset_universe_returns = asset_universe.pct_change()
portfolio_constituents_bootstrapping =
pd.DataFrame([((asset_universe_returns.iloc[random.choices(
range(len(asset_universe)), k=252)]).mean(axis=1)+1).cumprod().values
for x in range(1000)]).T
portfolio_constituents_bootstrapping.plot(figsize=figsize, legend=False, linewidth=1, alpha=0.2, color='purple')
plt.show()
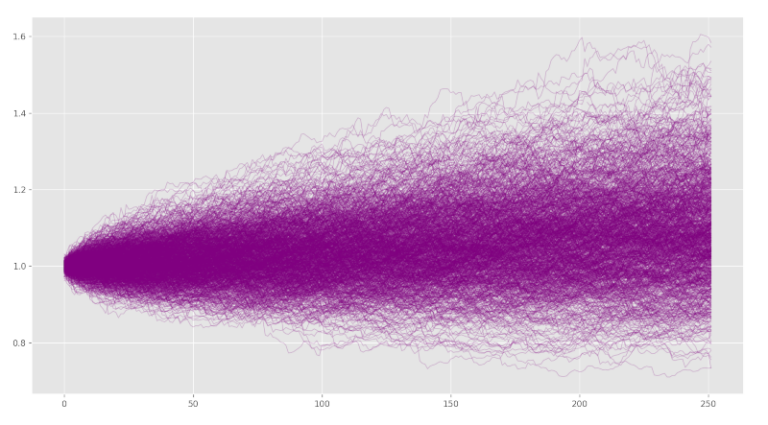
Infine vediamo come usare il metodo parametrico di Monte Carlo, e quindi confrontarlo con i risultati del Bootstrapping.
Analisi delle simulazioni Monte Carlo
Come affermato in precedenza, il metodo parametrico Monte Carlo usa le caratteristiche della popolazione sottostante per generare campioni casuali di valori. In questo caso le caratteristiche che ci interessano sono la media e la deviazione standard (o varianza) della distribuzione dei rendimenti storici. Questi valori sono inseriti in un modello che campiona casualmente da una distribuzione normale che ha la stessa media e deviazione standard della distribuzione dei rendimenti storici.
Calcoliamo quindi la media e la deviazione standard del portafoglio combinato di asset che abbiamo prodotto in precedenza.
mu = portfolio_returns.mean()
sigma = portfolio_returns.std()
print(f'Our portfolio mean return value is {round(mu*100,2)}%')
print(f'Our portfolio standard deviation value is {round(sigma*100,2)}%')
Our portfolio mean return value is 0.04%
Our portfolio standard deviation value is 0.84%
Generiamo quindi le serie casuali a partira da una distribuzione normale con media 0,04% e deviazione standard 0,84%.
portfolio_mc = pd.DataFrame([(np.random.normal(loc=mu, scale=sigma, size=252)+1) for x in range(1000)]).T.cumprod()
portfolio_mc.plot(figsize=figsize, legend=False, linewidth=1, alpha=0.2, color='green')
plt.show()
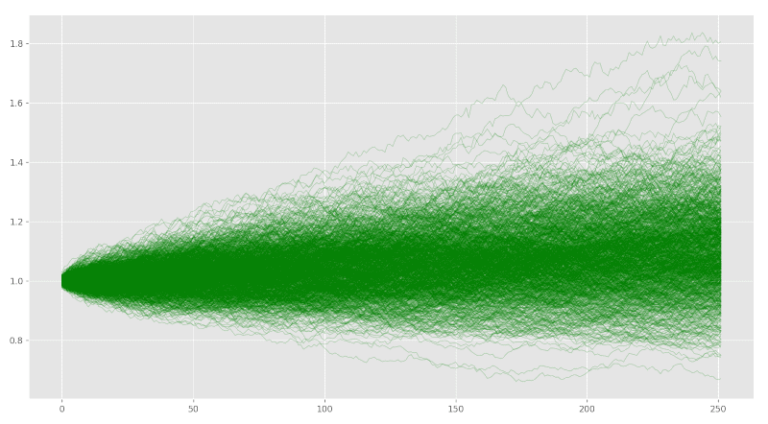
Finalmente possiamo effettuare la simulazione Monte Carlo creando estrazioni casuali da ogni singola distribuzione di asset. Costruiamo quindi il nostro portafoglio e verifichiamo se abbiamo risultati differenti dai precedenti.
for asset in (asset_universe_returns.mean() * 100).round(2).index:
print(f'The mean return for {asset} is {(asset_universe_returns.mean() * 100).round(2)[asset]}%')
print('\n')
for asset in (asset_universe_returns.std() * 100).round(2).index:
print(f'The standard deviation for {asset} is {(asset_universe_returns.std() * 100).round(2)[asset]}%')
The mean return for ^DJI is 0.04%
The mean return for ^IXIC is 0.06%
The mean return for ^GSPC is 0.04%
The mean return for ^STOXX50E is 0.02%
The mean return for ^N225 is 0.04%
The mean return for ^GDAXI is 0.04%
The standard deviation for ^DJI is 0.87%
The standard deviation for ^IXIC is 1.06%
The standard deviation for ^GSPC is 0.91%
The standard deviation for ^STOXX50E is 1.23%
The standard deviation for ^N225 is 1.27%
The standard deviation for ^GDAXI is 1.17%
Creiamo i dataframe dei rendimenti simulati per ogni singolo asset e li memorizziamo in una lista.
asset_returns_dfs = []
for asset in asset_universe_returns.mean().index:
mu = asset_universe_returns.mean()[asset]
sigma = asset_universe_returns.std()[asset]
asset_mc_rets = pd.DataFrame([(np.random.normal(loc=mu, scale=sigma, size=252)) for x in range(1000)]).T
asset_returns_dfs.append(asset_mc_rets)
Dobbiamo quindi scorrere la lista dei dataframe dei rendimenti degli asset e dividere i valori per il numero di asset. In questo modo otteniamo un portafoglio equi-pesato.
weighted_asset_returns_dfs = [(returns_df / len(tickers)) for returns_df in asset_returns_dfs]
reduce della libreria functools. Questa è un’ottima libreria, insieme alla libreria itertools, perchè dispone di molte funzioni utili e sicuramente vale la pena approfondirle.
portfolio_constituents_mc = (reduce(lambda x, y: x + y,weighted_asset_returns_dfs) + 1).cumprod()
Infine tracciamo il grafico dei valori dei portafoglio ottenuti dalle simulazioni Monte Carlo.
portfolio_constituents_mc.plot(figsize=figsize, legend=False, linewidth=1, alpha=0.2, color='orange')
plt.show()
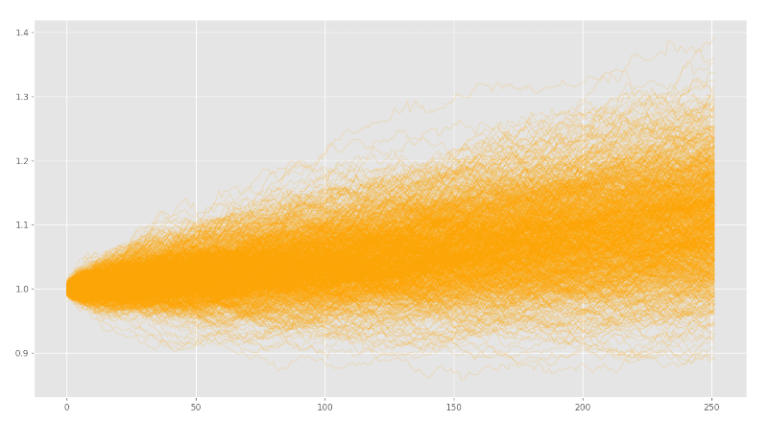
Possiamo vedere che qualcosa sembra diverso!! Forse non immediatamente, ma se guardiamo attentamente qualcosa dovrebbe saltarci all’occhio. Notiamo che tutte le simulazioni precedenti, sia Bootstrapping che Monte Carlo, hanno prodotto simulazioni i cui valori finali rientrano nei limiti tra 0,8-1,6. Nell’ultimo grafico vediamo che questi limiti si sono stretti tra circa 0,9-1,3.
Questa è una differenza significativa e non può essere attribuita agli effetti della sola casualità. Se ripetiamo tutte queste simulazioni alcune volte, vediamo che i risultati rimangono simili e l’ultimo metodo produce sempre un intervallo di valori finali più ristretto.
Effetto della correlazione
Ricordiamoci quando abbiamo menzionato gli effetti della correlazione tra i singoli asset e come abbiamo sottolineato la necessità di catturare questo effetto durante l’esecuzione delle simulazioni. La differenza dei valori finale dell’ultimo metodo è causata dal fatto che questo metodo non riesce a catturare questo effetto di correlazione.
Diamo un rapido sguardo alle correlazioni storiche tra i rendimenti degli asset che costituiscono l’universo degli asset che abbiamo scelto.
NOTA: è importante calcolare la correlazione tra i RENDIMENTI dell’asset, NON tra i loro prezzi.
Creiamo una piccola heatmap delle correlazione per avere una conferma visiva.
ax, fig = plt.subplots(figsize=(12,10))
sns.heatmap(asset_universe_returns.corr(),annot=True)
plt.plot()
plt.show()
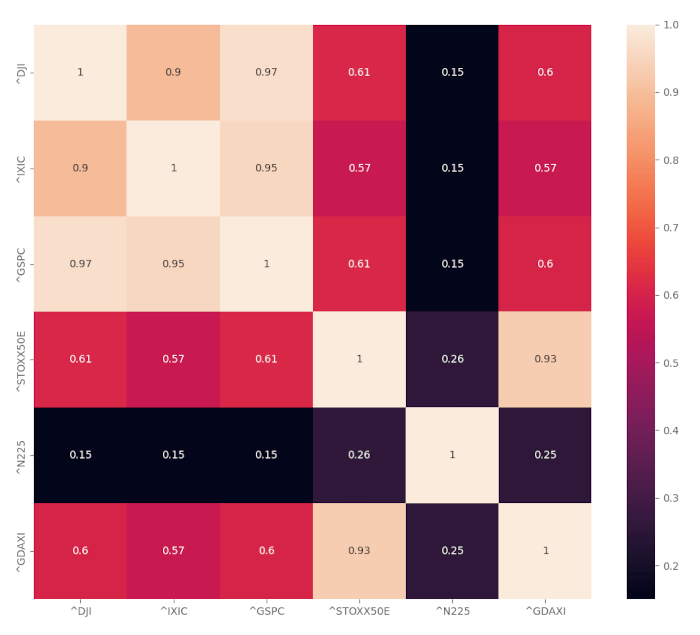
Possiamo vedere che tutti gli asset sono correlati positivamente in una certa misura, alcuni più di altri, ma soprattutto i valori sono tutti positivi. Questo spiega perché l’ultimo grafico e l’ultimo metodo di simulazione, cioè le simulazioni parametriche Monte Carlo sugli asset che conpongono il portafoglio, hanno prodotto un intervallo di valori finali più ristretto.
Il motivo è abbastanza semplice. Quando due asset sono correlati, tendono a muoversi nella stessa direzione allo stesso tempo, quindi se un asset ha un aumento di valore, generalmente anche l’altro ha un aumento. Quindi portafogli che contengono asset correlati positivamente hanno , in media, valori più estremi rispetto a un portafoglio di asset totalmente non correlati, o addirittura asset correlati negativamente.
Otteniamo questo risultato perché gli asset altamente correlati tendono a salire e scendere tutti allo stesso tempo, causando oscillazioni volatili nei valori. Quindi questo effetto ha causato la differenza nei risultati delle nostre simulazioni.
In particolare, i primi 3 approcci hanno catturato la correlazione intrinseca che esiste tra gli asset, mentre l’ultimo approccio non l’ha catturata.
L’approccio 1 ha creato il portafoglio usando i valori reali dei rendimenti storici giornalieri che si sono effettivamente verificati nei mercati nello stesso giorno. In questo caso gli andamenti incorporati erano movimenti reali generate dal processo sottostante ed è stato influenzato dalla reale correlazione tra gli asset.
Stessa logica per l’approccio 2, ma in questo caso abbiamo eseguito il bootstrap dei rendimenti per i nostri singoli asset e POI abbiamo formato il portafoglio. I rendimenti iniziali che erano stati sottoposti al bootstrap, sono stati nuovamente selezionati con cura in modo che tutti i rendimenti in una singola estrazione fossero presi nello stesso giorno di ciascun asset. In questo modo abbiamo assicurato che i valori estratti fossero valori reali che si sono effettivamente verificati in un solo giorno, e ancora una volta sono stati generati dal reale processo sottostante che implicitamente spiega la correlazione tra gli asset.
La differenza tra l’approccio 3 e 4 diventa leggermente più sottile.
Con l’approccio 3, abbiamo creato il nostro portafoglio usando i rendimenti reali dei singoli asset e POI abbiamo eseguito il processo MonteCarlo parametrico, simulando le serie dei rendimenti in base alle caratteristiche sottostanti del portafoglio. La parte è fondamentale è che la serie dei prezzi ha implicitamente rappresentato la correlazione tra gli asset perchè il portafoglio è stato creato PRIMA usando i valori reali dei rendimenti giornalieri equi-pesati dei singoli asset. In questo caso, quando abbiamo eseguito la simulazione Monte Carlo, abbiamo inserito parametri di input calcolati su una serie di prezzi storici che contenevano implicitamente le relazioni di correlazione. Quindi il metodo ha catturato gli effetti della correlazione.
Tuttavia, con l’approccio 4 non siamo riusciti a modellare correttamente l’effetto della correlazione. Le singole simulazioni Monte Carlo per ciascun asset venivano alimentate con parametri calcolati sulla base di valori calcolati completamente indipendenti l’uno dall’altro. Il calcolo della media e della deviazione standard di un asset è stato eseguito nel “vuoto”, cioè in modo completamente indipendente dagli altri asset.
In altre parole, usare le estrazioni effettuate da una distribuzione normale significa che i valori estratti ogni giorno per ogni singolo asset sono effettivamente “casuali”. In questo modo abbiamo la stessa probabilità di avere un risultato positivo o negativo per ogni singolo asset, indipendentemente dall’output degli altri asset.
Questo è molto simile a quello che ci aspetteremmo da una serie di asset completamente non correlati: ognuno si muove in modo casuale, indipendentemente dalle mosse degli altri. Così all’improvviso abbiamo iniziato a modellare la serie dei prezzi simulati di un paniere di attività non correlate!
Non è quello che vogliamo. quindi dobbiamo fare attenzione quando eseguiamo questi approcci e assicurarci di modellare correttamente il comportamento reale degli asset.
Codice completo
In questo articolo abbiamo esaminato e confrontato l’analisi Monte Carlo e Bootstrapping con Python. Per il codice completo riportato in questo articolo, si può consultare il seguente repository di github:
https://github.com/datatrading-info/AnalisiDatiFinanziari