BACKTEST DI STRATEGIE

Strategia di pairs trading con il filtro di kalman in Python

Scritto da
Gianluca

In questo articolo rivisitiamo i concetti per implementare il backtest di una strategia di pairs trading con il filtro di Kalman in Python su coppie di titoli azionari co-integrati. La teoria alla base di questa strategia, come già descritto in precedenti articoli, prevede che i titoli azionari statisticamente co-integrate si muovono in modo direttamente correlato. Quando i loro prezzi iniziano a divergere fino ad una certa soglia (cioè aumenta lo spread tra i prezzi delle 2 azioni), ci aspettiamo che i prezzi iniziano a ritornare verso la media ed infine convergere nuovamente.

La strategia di pairs trading

In questo scenario, la strategia prevede di vendere il titolo con prestazioni superiori e acquistare il titolo con prestazioni inferiori. Ci aspettiamo che il titolo con prestazioni inferiori dovrà “recuperare” il titolo con prestazioni superiori e quindi aumentare di prezzo. Viceversa il titolo con prestazioni superiori dovrà tornare verso la media e quindi risentire di una pressione al ribasso che diminuisce il valore relativo del titolo.

Il pairs trading è una strategia di trading neutrale al mercato che permette ai trader di trarre profitto praticamente da qualsiasi condizione di mercato: trend rialzista, trend ribassista o movimento laterale.

Dobbiamo prima individuare le azioni co-integrate. A tale scopo la teoria economica suggerisce che abbiamo più probabilità di trovare coppie di azioni guidate dagli stessi fattori, se cerchiamo tra i titoli azionari dello stesso settore o settori simili. Dopotutto, è logico aspettarsi che 2 titoli del settore tecnologico con prodotti simili, subiscono gli stessi alti e bassi generati nell’ambiente industriale.

Verifichiamo questa teoria effettuando il backtest su un paniere di titoli tecnologici. A tale scopo dobbiamo estrarre la lista dei ticker da un sito web (ad es, makerwatch) e quindi scaricare le serie storiche dei prezzi da Yahoo Finance.

Su DataTrading.info abbiamo già descritto questo argomento: il pairs trading basato sul ritorno verso la media. In questo articolo non vogliamo ripeterci ma aggiungere ulteriori elementi non presenti negli articoli principali.

In particolare vediamo come:

Creare una heatmap di coppie co-integrate in modo avere una rappresentazione visiva dei livelli di cointegrazione tra tutte le coppie di ticker.
Introduciamo il concetto di “Filtro di Kalman” quando analizziamo la serie degli spread che fornisce i segnali di trading.
Aggiungere i concetti di “set di addestramento” dei dati e di “set di test” dei dati, separando i due. In questo modo possiamo evitare il “lookahead bias”. Questo accade quando testiamo la cointegrazione sull’intero set di dati ed eseguiamo il backtest della strategia di trading sullo stesso set di dati. Dopo tutto, come possiamo eseguire un test di cointegrazione su un periodo di tempo per selezionare le nostre coppie di trading, e quindi viaggiare indietro nel tempo ed eseguire negoziazioni nello stesso periodo di tempo. Questo non è possibile, ma è una sottile trappola in cui cadono molti, molti trader sistematici.

Il filtro di Kalman

Il concetto alla base del filtro di Kalman afferma che:

Possiamo usare un filtro di Kalman in qualsiasi luogo dove abbiamo informazioni incerte su un sistema dinamico e possiamo fare un’ipotesi plausibile sul comportamento futuro del sistema. Anche se nella realtà abbiamo del rumore che interferisce con il movimento ordinato previsto dal sistema, il filtro di Kalman spesso aiuta a capire cosa il vero movimento del sistema. Possiamo quindi sfruttare le correlazioni tra questi fenomeni.
I filtri di Kalman sono ideali per i sistemi che cambiano continuamente. Hanno il vantaggio di essere leggeri computazionalmente (non hanno bisogno di conservare alcuna cronologia diversa dallo stato precedente) e sono molto veloci, il che li rende adatti per problemi in tempo reale e sistemi embedded.

Iniziamo ad importare le librerie pyhon necessari per implementare il backtest di questa strategiaQuindi iniziamo a importare i moduli pertinenti di cui avremo bisogno per il nostro backtest strategico:

				
					

import math
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib as mpl
mpl.style.use('bmh')
import matplotlib.pylab as plt
from datetime import datetime
import statsmodels.api as sm
from pykalman import KalmanFilter
import yahooquery

Usiamo Pandas e la libreria yahooquery per ottenere una lista di ticker di titoli azionari appartenenti al settore tecnologico.

				
					
# Otteniamo il risultato dello screener di yahoo per il settore tecnologico per i primi 30 ticker
s = yahooquery.Screener()
data = s.get_screeners('information_technology_services', count=30)
# Inseriamo il risultato in un dataframe Pandas
df = pd.DataFrame(data['information_technology_services']['quotes'])
# Creiamo la lista dei ticker dal dataframe
stocks = df['symbol'].dropna().tolist()
# Creaiamo una lista vouta per memorizzare i prezzi storici dei ticker
df_list = []
# Creiamo una lista dei ticker per cui abbiamo ottenuto i dati storici
used_stocks = []
# Ciclo sulla lista dei ticker per scaricari i dati storici e memorizzarli in una lista
for stock in stocks:
    try:
        data = yahooquery.Ticker(stock).history(start='2010-01-01', end='2020-01-01')['close']
        data.reset_index(level=0, drop=True, inplace=True)
        data.name = stock
        df_list.append(data)
        used_stocks.append(stock)
    except:
        pass
# Concatena la lista dei dataframe individuali dei prezzi dei ticker in un unico dataframe
df = pd.concat(df_list, axis=1)
# Rimuoviamo tutti i ticker che non hanno abbastanza storico nel periodo considerato
df = df.dropna(axis=1)

Visualizziamo il grafico dei dati dei prezzi solo per assicurarci di avere ciò di cui abbiamo bisogno e per un rapido controllo di integrità:

				
					
df.plot(figsize=(20,10))

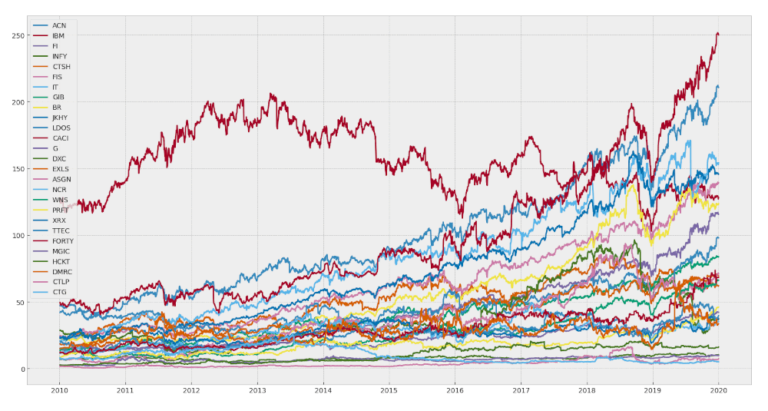
Dal grafico vediamo che abbiamo scaricato i dati storici dei prezzi per circa 25-30 azioni, che dovrebbero essere sufficienti per trovare almeno un paio di coppie co-integrate su cui eseguire il backtest.

Implementiamo ora una funzione che elabora i ticker, combinandoli in coppie univoche ed eseguire il test di cointegrazione su ciascuna coppia. I risultati sono memorizzati in una matrice e visualizzati con una heatmap. Inoltre, se il test di cointegrazione soddisfa la soglia di significatività statistica (il 5% nel nostro caso), allora memorizziamo la coppia di ticker azionari in una lista per analisi successive.

				
					

# LA SOGLIA CRITICA PER IL TEST DI COINTEGRAZIONE E' STATO IMPOSTATO AL 5%
def find_cointegrated_pairs(dataframe, critial_level=0.05):
    n = dataframe.shape[1]  # lunghezza del dateframe
    pvalue_matrix = np.ones((n, n))  # inizializza la matrice dei risultati
    keys = dataframe.columns  # ottiene il nome delle colonne
    pairs = []  # inizializza la lista delle coppie di ticker
    for i in range(n):
        for j in range(i + 1, n):  # con j > i
            stock1 = dataframe[keys[i]]  # prezzi dello "stock1"
            stock2 = dataframe[keys[j]]  # prezzi dello "stock2"
            result = sm.tsa.stattools.coint(stock1, stock2)  # calcolo cointegrazione
            pvalue = result[1]  # memorizza il p-value
            pvalue_matrix[i, j] = pvalue
            if pvalue < critial_level:  # se il p-value è minore della soglia
                pairs.append((keys[i], keys[j], pvalue))  # memorizza la coppia di ticker con il p-value
    return pvalue_matrix, pairs

Elaboriamo i dati storici dei prezzi con la funzione di cointegrazione, salviamo i risultati e tracciamo la heatmap.

				
					
# Imposta lo split point per i "dati di addestramento" su cui eseguire il test di co-integrazione
# (i restanti dati verranno inviati alla funzione di backtest)
split = int(len(df) * .4)
# esegue la funzione di cointegrazionerun sul dataframe dei dati di addestramento
pvalue_matrix, pairs = find_cointegrated_pairs(df[:split])
# converte la matrice dei risultati in un dataframe
pvalue_matrix_df = pd.DataFrame(pvalue_matrix)
# usa Seaborn per il grafico della heatmap dei risultati
fig, ax = plt.subplots(figsize=(15, 10))
sns.heatmap(pvalue_matrix_df, xticklabels=df.columns.to_list(), yticklabels=df.columns.to_list(), ax=ax)

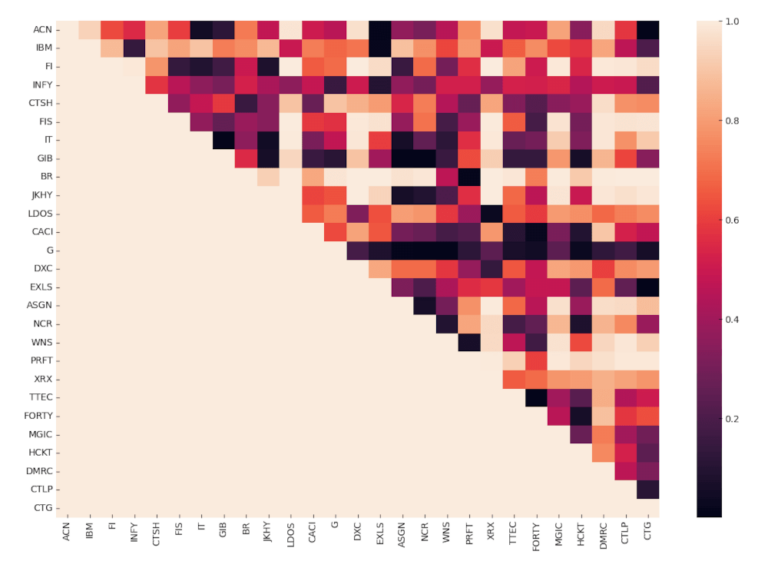
Dalla heatmap possiamo vedere riquadrati rossi molto scuri che segnalano effettivamente la presenza di alcune coppie di azioni con punteggio di cointegrazione al di sotto della soglia del 5%. Per avere un’indicazione più esplicita, stampiamo la lista delle coppie che rientrano all’interno della soglia.

				
					
for pair in pairs:
    print("Stock {} and stock {} has a co-integration score of {}".format(pair[0], pair[1], round(pair[2], 4)))

				
					Stock ACN and stock IT has a co-integration score of 0.0479
Stock ACN and stock EXLS has a co-integration score of 0.016
Stock ACN and stock CTG has a co-integration score of 0.0012
Stock IBM and stock EXLS has a co-integration score of 0.0186
Stock IT and stock GIB has a co-integration score of 0.0078
Stock GIB and stock ASGN has a co-integration score of 0.0044
Stock GIB and stock NCR has a co-integration score of 0.0022
Stock BR and stock PRFT has a co-integration score of 0.014
Stock LDOS and stock XRX has a co-integration score of 0.0357
Stock CACI and stock FORTY has a co-integration score of 0.0218
Stock G and stock ASGN has a co-integration score of 0.0133
Stock G and stock NCR has a co-integration score of 0.0084
Stock G and stock WNS has a co-integration score of 0.0063
Stock G and stock FORTY has a co-integration score of 0.0493
Stock G and stock HCKT has a co-integration score of 0.0336
Stock EXLS and stock CTG has a co-integration score of 0.0013
Stock TTEC and stock FORTY has a co-integration score of 0.0007

Usiamo un paio di funzioni della libreria pykalman per generare i filtri di Kalman da applicare alle coppie cointegrate e, a sua volta, la regressione che è alimentata dai dati delle suddette coppie.

Inoltre definiamo una funzione Halflife dove usiamo una parte del codice descritto in un precedente articolo relativo al trading mean-reverting.

				
					# Regressione con filtro di Kalman
def KalmanFilterRegression(x, y):
    delta = 1e-3
    trans_cov = delta / (1 - delta) * np.eye(2)  # Oscillazione della random walk
    obs_mat = np.expand_dims(np.vstack([[x], [np.ones(len(x))]]).T, axis=1)
    kf = KalmanFilter(n_dim_obs=1, n_dim_state=2,  # y è a 1 dimensione, (alpha, beta) è a 2 dimensioni
                      initial_state_mean=[0, 0],
                      initial_state_covariance=np.ones((2, 2)),
                      transition_matrices=np.eye(2),
                      observation_matrices=obs_mat,
                      observation_covariance=2,
                      transition_covariance=trans_cov)
    # Usare l'osservazione y per ottenere le stime e gli errori per i parametri dello stato
    state_means, state_covs = kf.filter(y.values)
    return state_means


def half_life(spread):
    spread_lag = spread.shift(1)
    spread_lag.iloc[0] = spread_lag.iloc[1]
    spread_ret = spread - spread_lag
    spread_ret.iloc[0] = spread_ret.iloc[1]
    spread_lag2 = sm.add_constant(spread_lag)
    model = sm.OLS(spread_ret, spread_lag2)
    res = model.fit()
    halflife = int(round(-np.log(2) / res.params[1], 0))
    if halflife <= 0:
        halflife = 1
    return halflife

Il backtest della strategia

Definiamo ora la funzione principale per il backtest di una strategia di pairs trading con il filtro di Kalman in Python. La funzione accetta una coppia di ticker alla volta e restituisce diversi output, cioè il dataframe dei rendimenti cumulativi, lo Sharpe Ratio e il Compound Annual Growth Rate (CAGR). Dobbiamo quindi iterare la lista di coppie, eseguendo la funzione con i dati relaviti di ogni coppia e memorizzare i risultati di ogni coppia per analisi successivi.

				
					
def backtest(df,s1, s2):
    #############################################################
    # INPUT:
    # DataFrame dei prezzi
    # s1: il simbolo del ticker 1
    # s2: il simbolo del ticker 2
    # x: la serie dei prezzi del ticker 1
    # y: la serie dei prezzi del ticker 2
    # OUTPUT:
    # df1['cum rets']: i rendimenti comulativi in un dataframe pandas
    # sharpe: Sharpe ratio
    # CAGR: Compound Annual Growth Rate
    x = df[s1]
    y = df[s2]
    # esecuzione della regressione (compreso il filtro di Kalman)
    # per trovare il hedge ratio e creare la serie degli spread
    df1 = pd.DataFrame({'y':y,'x':x})
    df1.index = pd.to_datetime(df1.index)
    state_means = KalmanFilterRegression(KalmanFilterAverage(x),KalmanFilterAverage(y))
    df1['hr'] = - state_means[:,0]
    df1['spread'] = df1.y + (df1.x * df1.hr)
    # calcolo half life
    halflife = half_life(df1['spread'])
    # calcolo dello z-score con la finestra del periodo pari a half life
    meanSpread = df1.spread.rolling(window=halflife).mean()
    stdSpread = df1.spread.rolling(window=halflife).std()
    df1['zScore'] = (df1.spread-meanSpread)/stdSpread
    ##############################################################
    # LOGICA DELLA STRATEGIA
    entryZscore = 2
    exitZscore = 0
    # impostazione dei setup long
    df1['long entry'] = ((df1.zScore < - entryZscore) & ( df1.zScore.shift(1) > - entryZscore))
    df1['long exit'] = ((df1.zScore > - exitZscore) & (df1.zScore.shift(1) < - exitZscore))
    df1['num units long'] = np.nan
    df1.loc[df1['long entry'], 'num units long'] = 1
    df1.loc[df1['long exit'], 'num units long'] = 0
    df1['num units long'].iat[0] = 0
    df1['num units long'] = df1['num units long'].fillna(method='pad')
    # impostazione dei setup short
    df1['short entry'] = ((df1.zScore > entryZscore) & ( df1.zScore.shift(1) < entryZscore))
    df1['short exit'] = ((df1.zScore < exitZscore) & (df1.zScore.shift(1) > exitZscore))
    df1.loc[df1['short entry'], 'num units short'] = -1
    df1.loc[df1['short exit'], 'num units short'] = 0
    df1['num units short'].iat[0] = 0
    df1['num units short'] = df1['num units short'].fillna(method='pad')
    df1['numUnits'] = df1['num units long'] + df1['num units short']
    df1['spread pct ch'] = (df1['spread'] - df1['spread'].shift(1)) / ((df1['x'] * abs(df1['hr'])) + df1['y'])
    df1['port rets'] = df1['spread pct ch'] * df1['numUnits'].shift(1)
    df1['cum rets'] = df1['port rets'].cumsum()
    df1['cum rets'] = df1['cum rets'] + 1
    ##############################################################
    sharpe = ((df1['port rets'].mean() / df1['port rets'].std()) * math.sqrt(252))
    if math.isnan(sharpe):
        sharpe = 0.0

    ##############################################################
    start_val = 1
    end_val = df1['cum rets'].iat[-1]
    start_date = df1.iloc[0].name
    end_date = df1.iloc[-1].name
    days = (end_date - start_date).days
    CAGR = round(((float(end_val) / float(start_val)) ** (252.0/days)) - 1,4)
    df1[s1+ " "+s2] = df1['cum rets']
    return df1[s1+" "+s2], sharpe, CAGR

Eseguiamo la funzione di Backtest per tuttel coppie della lista e stampiamo alcuni risultati durante l’esecuzione. Inoltre, dopo aver memorizzato l’equity di ogni coppia, produciamo un grafico che visualizza ogni curva di equity.

				
					results = []
for pair in pairs:
    rets, sharpe,  CAGR = backtest(df[split:], pair[0], pair[1])
    results.append(rets)
    print("The pair {} and {} produced a Sharpe Ratio of {} and a CAGR of {}".format(pair[0],pair[1],round(sharpe,2),round(CAGR,4)))
    rets.plot(figsize=(20,15),legend=True)

				
					The pair ACN and IT produced a Sharpe Ratio of 1.32 and a CAGR of 0.0311
The pair ACN and EXLS produced a Sharpe Ratio of 0.97 and a CAGR of 0.0094
The pair ACN and CTG produced a Sharpe Ratio of 1.26 and a CAGR of 0.0538
The pair IBM and EXLS produced a Sharpe Ratio of 1.46 and a CAGR of 0.0428
The pair IT and GIB produced a Sharpe Ratio of 1.46 and a CAGR of 0.0368
The pair GIB and ASGN produced a Sharpe Ratio of 0.97 and a CAGR of 0.0345
The pair GIB and NCR produced a Sharpe Ratio of 0.89 and a CAGR of 0.0109
The pair BR and PRFT produced a Sharpe Ratio of 0.43 and a CAGR of 0.0052
The pair LDOS and XRX produced a Sharpe Ratio of 1.3 and a CAGR of 0.0598
The pair CACI and FORTY produced a Sharpe Ratio of 0.0 and a CAGR of 0.0
The pair G and ASGN produced a Sharpe Ratio of 0.95 and a CAGR of 0.0431
The pair G and NCR produced a Sharpe Ratio of 1.0 and a CAGR of 0.0448
The pair G and WNS produced a Sharpe Ratio of 0.78 and a CAGR of 0.0083
The pair G and FORTY produced a Sharpe Ratio of 0.0 and a CAGR of 0.0
The pair G and HCKT produced a Sharpe Ratio of 1.4 and a CAGR of 0.0711
The pair EXLS and CTG produced a Sharpe Ratio of 1.57 and a CAGR of 0.0554
The pair TTEC and FORTY produced a Sharpe Ratio of 0.0 and a CAGR of 0.0

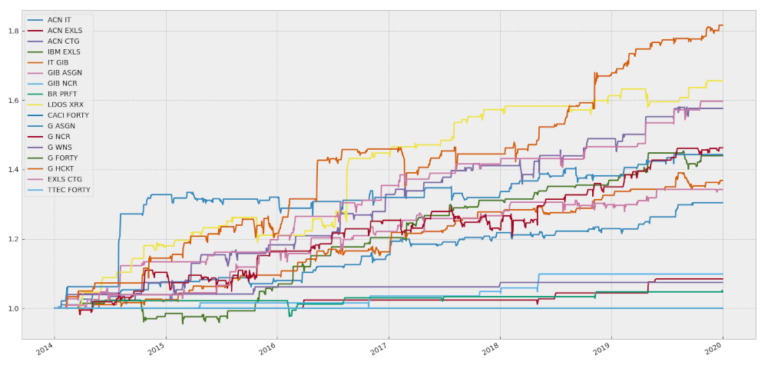
Infine, con alcune righe di codice extra, possiamo combinare e pesare equamente le equity delle singole coppie per visualizzare la curva di equity della strategia complessiva.

				
					
# Concatena le singole curve di equity in un solo dataframe
results_df = pd.concat(results,axis=1).dropna()
# Pesa equamente ogni equity dividendo per il numero di coppie nel dataframe
results_df /= len(results_df.columns)
# Somma le equity pesate per ottenere l'equity finale
final_res = results_df.sum(axis=1)
# Stampa il grafico della curva dell'equity finale
final_res.plot(figsize=(20,15))

				
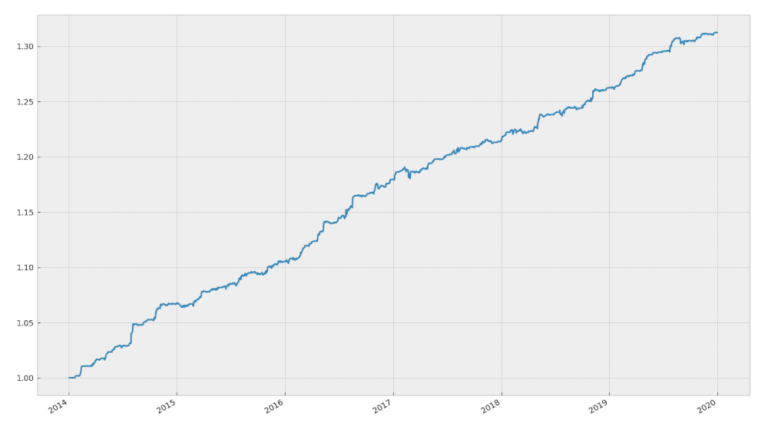
					# Calcola e stampa alcune statistiche dell'equity finale
sharpe = (final_res.pct_change().mean() / final_res.pct_change().std()) * (math.sqrt(252))
start_val = 1
end_val = final_res.iloc[-1]
start_date = final_res.index[0]
end_date = final_res.index[-1]
days = (end_date - start_date).days
CAGR = round(((float(end_val) / float(start_val)) ** (252.0/days)) - 1, 4)
print("Sharpe Ratio is {} and CAGR is {}".format(round(sharpe, 2), round(CAGR, 4)))

				
					Sharpe Ratio is 3.67 and CAGR is 0.0318

Codice completo

In questo articolo abbiamo descritto come implementare il backtest di una strategia di pairs trading con il filtro di Kalman in Python su coppie di titoli azionari co-integrati. Per il codice completo riportato in questo articolo, si può consultare il seguente repository di github:
https://github.com/datatrading-info/Backtest_Strategie