In questo articolo introduciamo un approccio di trading con il reinforcement learning in Python implementando una strategia che usa il machine learning per determinare quali operazioni eseguire. Prima di iniziare a esaminare la strategia, descriviamo uno degli algoritmi usati: Gradient Ascent.
Cos’è il Gradient Ascent
Il gradient ascent è un algoritmo usato per massimizzare una specifica funzione di ricompensa. Un semplice metodo per descrivere il gradient ascent è considerare il seguente scenario. Immaginiamo di essere bendati e posizionati da qualche parte su una montagna. Il compito è trovare il punto più alto della montagna. In questo scenario, la “funzione di ricompensa” che vogliamo massimizzare è la misura dell’altitudine. Per individuare il massimo possiamo semplicemente osservare la pendenza dell’area su cui ci si trova e spostarsi in salita. Seguire queste indicazioni un passo alla volta ci porterà alla cima, prima o poi!
Per salire verso la cima della montagna, è importante conoscere la pendenza, o gradiente, della zona, in modo da conoscere la direzione dove dirigersi. Il gradient è semplicemente la derivata della funzione di ricompensa rispetto ai suoi parametri.
Un’altra componente importante del gradient ascent è il learning rate. Questa componete rappresenta il numero di passi che facciamo prima di controllare nuovamente la pendenza. Troppi passi e potremmo superare la vetta; troppo pochi richiederebbe troppo tempo per raggiungere la cima. Allo stesso modo, un valore elevato di learning rate potrebbe portare l’algoritmo a divergere dal massimo, mentre un valore basso di learing rate potrebbe far sì che l’algoritmo impieghi troppo tempo per terminare.
Dopo aver descritto le basi del gradient ascent, vediamo come usarlo per eseguire un compito relativamente semplice: la regressione lineare.
Regressione lineare con il gradient ascent
Per prima cosa generiamo un dataset dove eseguire la regressione lineare.
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(1)
plt.rcParams["figure.figsize"] = (5, 3) # (w, h)
plt.rcParams["figure.dpi"] = 200
m = 100
x = 2 * np.random.rand(m)
y = 5 + 2 * x + np.random.randn(m)
plt.scatter(x, y)
plt.show()
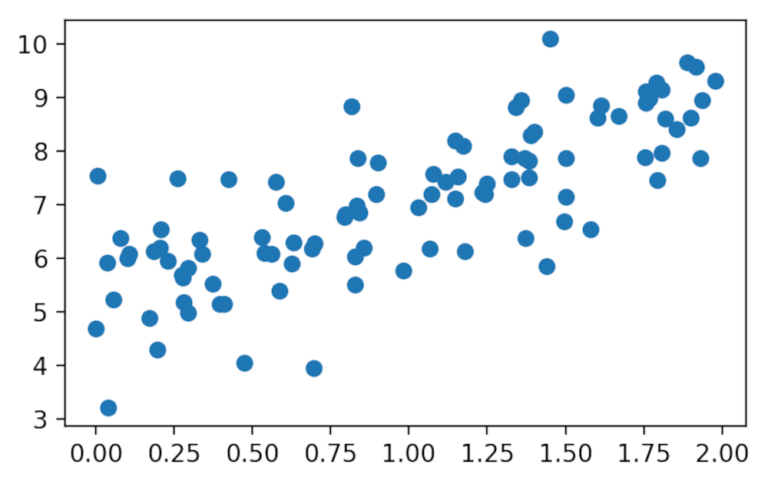
Abbiamo generato 100 punti casuali attorno ad una retta con un’intercetta di 5 e una pendenza di 2. Per completezza, possiamo trovare la retta più adatta tramite la funzione lingregress di Scipy.
from scipy.stats import linregress
slope, intercept = linregress(x, y)[:2]
print(f"slope: {slope:.3f}, intercept: {intercept:.3f}")
slope: 1.842, intercept: 5.237
Questi sono i valori da ottenere tramite l’algoritmo del gradient ascent.
Funzione di ricompensa
Il prossimo passo è definire la funzione di ricompensa. Una funzione comunemente usata per misurare l’accuratezza della regressione lineare è l’errore quadratico medio (MSE). L’MSE è la “media delle differenze tra i quadrati dei valori stimati e i quadrati dei valori osservati”. Poiché MSE è una funzione di errore e stiamo cercando una funzione da massimizzare, usiamo l’MSE negativo come funzione di ricompensa, \(J\).
\(J(\theta) = – {1 \over m} \sum\limits_{i=1}^{m}(\theta _{0} + \theta _{1}x^{(i)} – y^{(i)})^2\)
Dove \(\theta\) è il vettore dei parametri di input, in questo caso l’intercetta e la pendenza della linea che stiamo testando. Questa equazione può essere implementata in Python come segue:
x = np.array([np.ones(m), x]).transpose()
def accuracy(x, y, theta):
return - 1 / m * np.sum((np.dot(x, theta) - y) ** 2)
Il codice crea una matrice \(x\) dove \(x_0 = 1\) e \(x_1\) sono i valori originali x. In questo modo possiamo calcolare \(\theta_ {0} + \theta_ {1} x\) come \(\theta \cdot x\).
Funzione gradiente
Dopo aver definito la funzione di ricompensa, possiamo calcolare la funzione gradiente come la derivata parziale di \(J\) rispetto with \(\theta\):
\({\partial J(\theta)\over \partial\theta} = – {2 \over m} \sum\limits_{i=1}^{m}(\theta _{0} + \theta _{1}x^{(i)} – y^{(i)}) \cdot x^{(i)}\\)
Possiamo scrivere questa funzione in Python:
def gradient(x, y, theta):
return -1 / m * x.T.dot(np.dot(x, theta) - y)
Reinforcement Learning in Python
Siamo pronti per eseguire il gradient ascent. Impostiamo \(\theta\) pari a \([0, 0]\), o lo aggiorniamo ad ogni epoch, o passo, come:
\(\theta = \theta + \alpha{\partial J(\theta) \over \partial\theta}\)
dove \(\alpha\) è il learning rate.
num_epochs = 500
learning_rate = 0.1
def train(x, y):
accs = []
thetas = []
theta = np.zeros(2)
for _ in range(num_epochs):
# Memorizza tutti i valori di accuracy e theta nel tempo
acc = accuracy(x, y, theta)
thetas.append(theta)
accs.append(acc)
# aggiornamento theta
theta = theta + learning_rate * gradient(x, y, theta)
return theta, thetas, accs
theta, thetas, accs = train(x, y)
print(f"slope: {theta[1]:.3f}, intercept: {theta[0]:.3f}")
slope: 1.843, intercept: 5.236
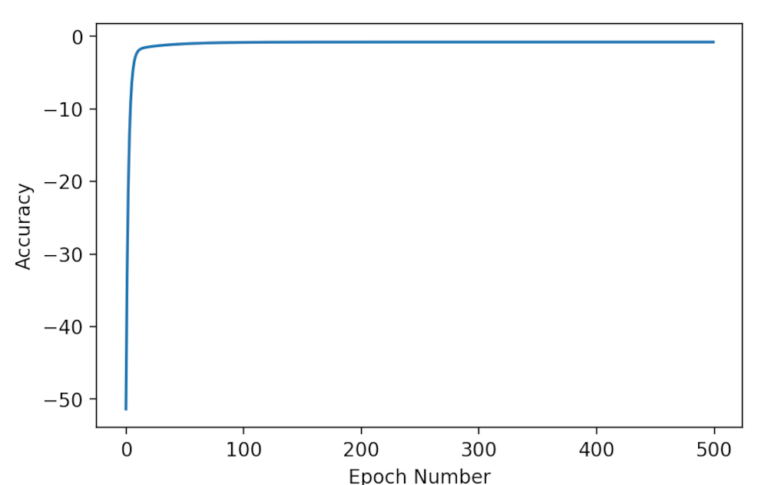
Abbiamo eguagliato il benchmark della regressione lineare! Se rappresentiamo graficamente l’accuratezza nel tempo, possiamo vedere che l’algoritmo converge rapidamente alla massima accuratezza:
plt.plot(accs)
plt.xlabel('Epoch Number')
plt.ylabel('Accuracy');
plt.show()
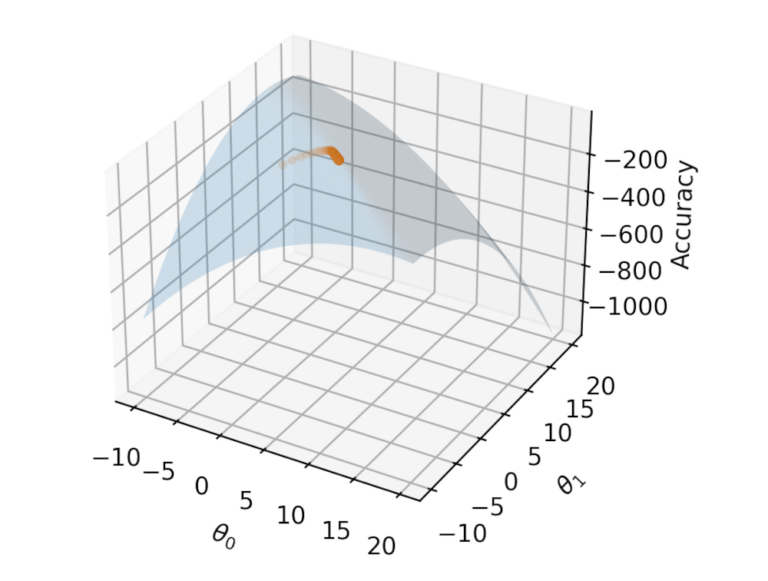
from mpl_toolkits.mplot3d import Axes3D
i = np.linspace(-10, 20, 50)
j = np.linspace(-10, 20, 50)
i, j = np.meshgrid(i, j)
k = np.array([accuracy(x, y, th) for th in zip(np.ravel(i), np.ravel(j))]).reshape(i.shape)
fig = plt.figure(figsize=(9,6))
ax = fig.add_subplot(projection='3d')
ax.plot_surface(i, j, k, alpha=0.2)
ax.plot([t[0] for t in thetas], [t[1] for t in thetas], accs, marker="o", markersize=3, alpha=0.1);
ax.set_xlabel(r'$\theta_0$')
ax.set_ylabel(r'$\theta_1$')
ax.set_zlabel("Accuracy")
plt.show()
Conclusione
In questo articolo abbiamo mostrato come usare il gradient ascent per massimizzare una funzione di ricompensa relativamente semplice con solo due parametri. Nel prossimo articolo descriviamo come applicare una funzione di ricompensa a una strategia di trading per addestrare un modello di trading algoritmico.
Codice completo
In questo articolo abbiamo descritto un approccio di trading con il reinforcement learning in Python. Per il codice completo riportato in questo articolo, si può consultare il seguente repository di github:
https://github.com/datatrading-info/MachineLearning